|
同步分层能力测试题(一)
A组
一.填空题(本大题共8小题,每小题5分,共40分)
1.在△ABC中, 若a= ,b= ,b=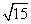 ,A=300,则边c= 。 ,A=300,则边c= 。
1. 2 或 或 。【解析】由余弦定理,得a2=c2+b2-2cb·cosA,代入整理得c2-3 。【解析】由余弦定理,得a2=c2+b2-2cb·cosA,代入整理得c2-3 c+10=0, c+10=0,
∴c=2 或 或 。 。
2. 在△ABC中,已知A=45 ,B=60 ,B=60 ,c =1,则a= . ,c =1,则a= .
2. 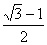 。【解析】由A+B+C=180,得 C=180 。【解析】由A+B+C=180,得 C=180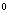 -45 -45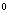 -60 -60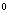 =75 =75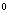 。由正弦定理,得 。由正弦定理,得
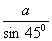 = =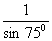 , ,  a= a=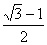 。 。
3. 在△ABC中, 已知a=5,b=12,c=13.最大内角为 度。
3.90.【解析】cosC=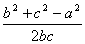 = = 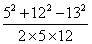 =0,C=900. =0,C=900.
4. 在△ABC中,已知b=4,c=8,B=30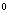 .则a= 。 .则a= 。
4. 2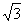 。【解析】(1)由正弦定理,得sin C= 。【解析】(1)由正弦定理,得sin C=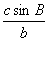 = =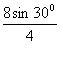 =1。所以 C=90 =1。所以 C=90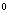 , ,
A=180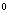 -90 -90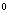 -30 -30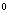 =60 =60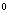 。又由正弦定理,得 a= 。又由正弦定理,得 a=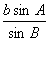 = = =2 =2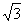 。 。
5. a,b,c是△ABC的三边,且B=1200,则a2+ac+c2-b2的值为 .
5.0.【解析】由余弦定理,得b2=a2+c2-2ac·cosB= a2+ac+c2.
6.在△ABC中,若a=50,b=25, A=45°则B= .
6. 60°或120°。【解析】由正弦定理得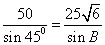 ,sinB= ,sinB=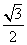 ,故B=60°或120°。 ,故B=60°或120°。
7.在△ABC中,有等式:①asinA=bsinB;②asinB=bsinA;③acosB=bcosA;④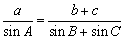 . 其中恒成立的等式序号为_______________. . 其中恒成立的等式序号为_______________.
7.②④。【解析】①不符合正弦定理;②两边同除以sinAsinB即为正弦定理;③取A=900,便知等式不成立;④正弦定理结合等比定理可得。 |

