|
章节能力测试题(一)
(测试范围:解三角形)
一.填空题(本大题共14小题,每小题5分,共70分)
1.三角形ABC中,如果A=60º,C=45º,且a= ,则c= 。 ,则c= 。
1.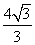 。提示:由正弦定理得 。提示:由正弦定理得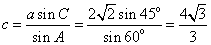 。 。
2. 在 △ABC中,C= △ABC中,C= ,则 ,则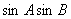 的最大值是_______________。 的最大值是_______________。
2.  。提示: 。提示: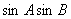 = =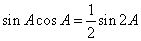 ,故 ,故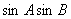 的最大值是 的最大值是 。 。
3.在△ABC中,若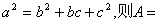 _________。 _________。
3. 1200.提示: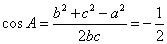 ,A=1200. ,A=1200.
4.在△ABC中,若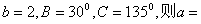 _________。 _________。
4.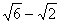 。提示:A=1800-300-1350=150.sin150=sin(450-300)= 。提示:A=1800-300-1350=150.sin150=sin(450-300)=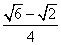 .由正弦定理得 .由正弦定理得 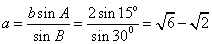 . .
5. 三角形的两边分别为5和3,它们夹角的余弦是方程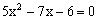 的根,则三角形的另一边长为 . 的根,则三角形的另一边长为 .
5. 2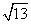 .提示:∵三角形两边夹角为方程 .提示:∵三角形两边夹角为方程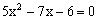 的根,不妨假设该角为 的根,不妨假设该角为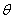 ,则易解得得 ,则易解得得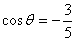 或 或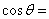 2(舍去),∴据余弦定理可得 2(舍去),∴据余弦定理可得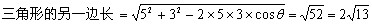 。 。
6.在△ABC中,已知a=5, c=10, A=30°, 则∠B= 。
6.B=105º或B=15º。提示:由正弦定理可得sinC=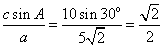 ,∴C=45º或者C=135º,∴B=105º或者B=15º。 ,∴C=45º或者C=135º,∴B=105º或者B=15º。
7.科学家发现,两颗恒星A与B分别与地球相距5亿光年与2亿光年,且从地球上观测,它们的张角为60º,则这两颗恒星之间的距离为 亿光年。
7. 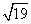 。解:设地球为O,则根据条件,OA=5,OB=2,∠AOB=60º,再利用余弦定理可得: 。解:设地球为O,则根据条件,OA=5,OB=2,∠AOB=60º,再利用余弦定理可得: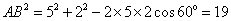 ,故AB= ,故AB=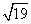 。 。
8. 在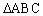 中, 中,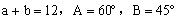 ,则 ,则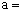 _______, _______,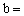 ________。 ________。
8. 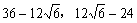 。提示: 。提示: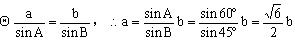 , ,
又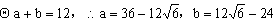 。 。
9. 在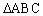 中,化简 中,化简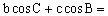 ___________ ___________
9. a。提示:利用余弦定理,得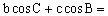 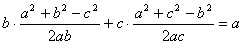 。 。
10. 在 ABC中,已知 ABC中,已知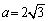 , ,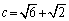 , ,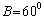 ,则A= 。 ,则A= 。
10.600.提示:∵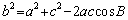 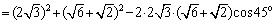 = =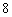 , ,
∴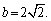 又∵sin 又∵sin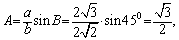 又∵ 又∵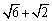 > >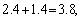
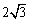 < <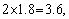 ∴ ∴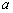 < <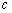 ,即 ,即 < <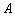 < <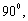 ∴ ∴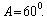
11.在等腰三角形 ABC中,已知sinA∶sinB=1∶2,底边BC=10,则△ABC的周长是 。
11.50.提示:据题意,等腰三角形ABC中,顶角为A,底角B=C,∴A+2B=π,即A=π-2B,又∵sinA∶sinB=1∶2,∴sin(π-2B):sinB=1:2,即sin2B:sinB=1:2,解得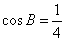 ,再据条件:底边BC=10,∴三角形腰长AB=AC= ,再据条件:底边BC=10,∴三角形腰长AB=AC=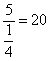 ,∴该三角形的周长是50。 ,∴该三角形的周长是50。 |

