|
从前有一个狡猾的地主,他把一块长为x米的正方形土地租给张老汉种植,有一天,他对张老汉说:“我把这块地的一边减少5米,另一边增加5米,继续租给你,你也没吃亏,你看如何?”张老汉一听觉得没有吃亏,就答应了.同学们,你能告诉张老汉他吃亏了吗?
计算下列各题:
(1)(x+2)(x-2)(2)(1+3a)(1-3a)
(3)(x+5y)(x-5y)(4)(y+3z)(y-3z)
1.平方差公式的推导
(a+b)(a-b)=a2-ab+ab-b2(多项式乘法法则)
=a2-b2(合并同类项)
2.平方差公式:(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积等于这两个数的平方差.
平方差公式结构特征:①左边是两个二项式相乘,这两个二项式中有一项完全相同,另
一项互为相反数.②右边是乘式中两项的平方差.即相同的平方与相反项的平方的差.
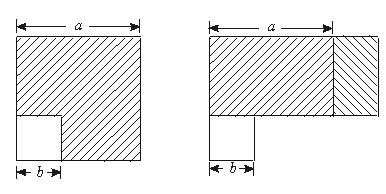
3.图形验证(a+b)(a-b)=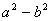 . .
下列各式都能用平方差公式吗? (课件)
- (a-3)(a+3) ( )
- (a+3)(a-2) ( )
C. (-a+3)(-a-3) ( )
D. (a+3)(-a-3) ( )
E. (-a-3)(a-3) ( )
能否用平方差公式,你有什么更快更好的判断方法吗?
两个多项式中:
两项相等,两项互为相反数
在平方差这个结果中谁作被减数,谁作减数,你还有什么办法确定?
相等数的平方减去相反数的平方
公式的主要作用是简化运算:现在我们掌握了公式的特点,就可以更快更准确地去运算了.请看例题:
[例1]计算:
(1).(2x+ )(2x- )(2x- ) (2). (1)(2x+y)(2x-y) ) (2). (1)(2x+y)(2x-y)
(3)(3a+2b)(3a-2b) (4)(200+1)(200-1)
例2]计算:
(1)(x+6)(6-x) (2) 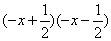 毛 毛
(3)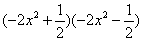 (4) (4)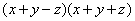
(5)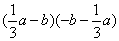 (6)(3a+b-2)(3a-b+2) (6)(3a+b-2)(3a-b+2)
(7)(3a-2b)(2b+3a) (8)(-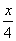 +y)( +y)( 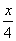 +y) +y)
(9)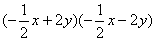 (10)(-4a-1)(4a-1) (10)(-4a-1)(4a-1)
例3]计算:
`1998×2002 999×1001 59.8×60.2
(1)498×502 (2)
1.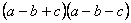 ; ;
2.求 的值,其中 的值,其中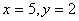 . .
3.若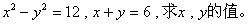
1、 本节课我们学了什么?
2、 公式有什么作用?
3、 公式如何使用,注意什么?
4、 公式的证明用的是数形结合(等面积法)的方法,这是今后我们常用的方法.
课本:
练习册:
|

