|
§13.3 一次函数与一次方程、一次不等式(2)
一、教学目标
(一) 知识与技能
1. 理解一次函数与一次不等式之间的关系。
2.会利用一次函数图象解决相关的一次不等式。
(二)过程与方法
通过探究一次函数与一次不等式之间的关系,体验数形结合这种重要的思想方法。
(三)情感目标
通过实例探究,培养学生深入探究的学习精神;通过一次函数与一次不等式之间关系的探究,使学生对所学知识进行融会贯通,深化对数形结合思想的理解。
二、教学重点
探究一次函数与一次不等式之间的关系。
三、教学难点
利用一次函数图象解一次不等式
四、教学方法
引导法,探究法,讨论法,数形结合法.
五、教学用具多媒体
六、教学过程
(一)创设情境,导入新课
对于一次函数y=kx+b(k、b为常数,且k≠0)当y>0或 y<0时,即kx+b>0 ,kx+b<0这时一次函数可以看成是一个关于未知数x的一元一次不等式,说明一次函数与一次不等式之间可能存在着一定的联系。
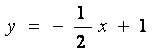 (二)合作交流、解读新课 (二)合作交流、解读新课
问题:x为何值时数,函数 值y=0,当自变量为何值时y>0,当自变量为何值时y>1。
探究与讨论:你有几种方法解出问题?
根据你的经验,你能迅速解答下列问题吗?
练习:1、作出函数y=3x-6的图象,用图象法求出当x取何值时,
(1)3x-6>0 (2)3x-6<0
2、用直接解不等式的方法求上题中的有两个不等式的解集,并比较两种方法的结果相同吗?
自主学习
1、作出函数y=2x-5的图象,观察图象回答下列问题:
(1)x取哪些值时,2x-5>0?
(2)x取哪些值时,2x-5<0? (3)x取哪些 |

