|
一、 复习旧知,引入新课
1 用因式分解法解方程x2-4=0。
2 若将方程先移项,得:x2=4。你能直接得到该方程的解吗?其解是什么?
3 引入新课,板书课题。
二、[讲解新课]
1.了解直接开平方法解一元二次方程的概念。
将方程:x2-4=0,先移项,得:x2=4。
因此,x=± 2即,x1=2,x2=-2。
讲(或提问)到此,指出 :这种解某些一元二次方程的方法叫做开平方法。
2. 初步掌握直接开平方法解一元二次方程。
提问:用直接开平方法解下列方程:
1、x2-144=0; 2、x2-3=0;
3、x2+16=0; 4、x2=0。
(1、x1=12,x2=-12;2、x1= 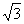 ,x2=- ,x2=-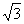 ;3、无解——负数没有平方根;4、x=0——0有一个平方根,它是0本身)。 ;3、无解——负数没有平方根;4、x=0——0有一个平方根,它是0本身)。
3. 深刻掌握直接开平方法解一元二次方程
例1 解方程:(1) 3x2-27=0 (2) (x+3)2=2。
说明与分析:此例要求解出方程的根,同时通过此例的学习也为进一步解公式法作准备。实际上,我们将用此例以及类似的题目推导出一元二次方程的另一解法——配方法。可以看出,原方程中x+3是2的平方根,
练习:解下列方程:
1、(x+4)2=3; 2、(3x+1)2=-3。
(1、x1=-4,x2=+ 4 ; 2、无解。)
4. 合作学习
(1) 想一想:你能用直接开平方法解方程x2+6x+7=0吗?
(2) 你能将方程x2+6x+7=0转化为(x+a)2=b的形式吗?
(3) 请与同伴尝试解这个方程。
5. 探索配方法解一元二次方程一般步骤
将方程:x2+6x+7=0的常数项移到右边,并将一次项6x改写成2·x·3,得:x2+2·x·3=-7。由此可以看出,为使左边成为完全平方式,只需在方程两边都加上32,即:x2+2·x·3+32=-7+32, (x+3)2=2。
解这个方程,得:x1=-3+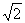 ,x2=-3- ,x2=-3-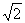 。 。
6. 总结配方法的概念:把一个一元二次方程左边配成一个完全平方式,右边为一个非负数,然后用开平方法求解,这种解一元二次方程的方法叫做配方法。
7. 做一做——进一步理解配方的过程。
填空:
1、x2+6x+ =(x+ )2; 2、x2-5x+ =(x- )2;
3、x2+ x+ =(x+ ), 2; 4、x2-9x+ =(x- )2
填空后总结配方的关键:对二次项系数为1的一元二次方程x2+bx=c配方,只需在方程两边都加上一次项系数一半的平方。
8. 教学例2 用配方法解下列一元二次方程
(1) x2+6x=1 (2) x2=6+5x
解答过程由学生口述,教师板书的形式完成。
通过例题2的讲解,帮助学生总结出配方的步骤: | 
