3．2 频数分布直方图 同步练习

解题示范

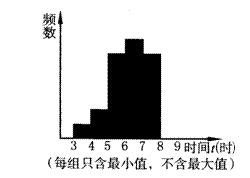例  某校课外活动小组为了解本校九年级学生的睡眠时间情况，对学校若干名九年级学生的睡眠时间进行了抽查，将所得数据整理后，画出了频数分布直方图的一部分，如图3-1，已知图中从左至右前5个小组的频率分别是0.04，0.08，0.24，0.28，0.24，第二小组的频数为4．

    请回答下列问题：

    （1）这次被抽查的学生人数是多少？并请补全频数分布直方图．

    （2）被抽查的学生中，睡眠时间在哪个范围内的人数最多？这一范围内的人数是多少？

    （3）如果该学校有900名九年级学生，若合理睡眠时间范围为7≤t<9，那么请你估计一下这个学校九年级学生中睡眠时间在此范围内的人数是多少？

    审题  已知五年小组的频率和其中一组的频数，要求抽查总数、余下一组的频率、最高频率组的频数以及待定范围内的频率和频数．

    方案  （1）由等式“频率＝”，可求出总数．由各组频率之和为1，可求出余下一组的频率，补全直方图．（2）补全直方图后，可以直接从图中观察出频率最高的一组，利用第（1）题中类似的方法求出对应的频数．（3）先计算出符合要求的频率之和，然后乘学生总数，即得到所求频数．

    实施  （1）∵第二小组的频数为4，频率为0.08，

    ∴这次被抽查的学生人数是4÷0.08=50（人）．

    第六小组的频率为1-0.04-0.08-0.24-0.28-0.24=0.12，频数为0.12×50=6．补全后的直方图略．

    （2）被抽查的学生睡眠时间在6≤t<7（第四小组）的人数最多．

    ∵0.28×50=14（人），∴ 这一范围内的人数是14人．

    （3）∵第五、六两组的频率之和为0.24+0.12=0.36，

     ∴0.36×900=324（人）．

    ∴估计这个学校九年级学生中睡眠时间在7≤t<9的人数约为324人．

    反思  要搞清楚频率、频数、总数三者的关系，并能灵活运用．要学会读直方图．