6.4 梯形(1)同步练习

解题示范

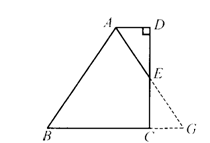例  如图，在梯形ABCD中，AD∥BC，DC⊥AD．AE平分∠BAD交CD于点E，且DE=EC．求证：AB=AD+BC．

    审题  本题是在梯形ABCD中证明线段的和差问题，提供的条件也较为丰富，如AD∥BC，DC⊥AD，AE平分∠BAD，且DE=EC，因此运用全等三角形不难解决此题．

    方案  延长AE，BC相交于点G，从而构造了△ADE≌△GCE，得AD=CG．由AE平分∠BAD，可得∠DAE=∠BAE．由AD∥BC，可得∠DAE=∠G．于是∠BAE=∠G，得到AB=BE．通过等量代换得AB=BC+CG=BC+AD．

    实施  延长AE，BC相交于点G．

    ∵AD∥BC，∴∠DAE=∠G．

    ∵∠DAE=∠BAE，∴∠BAE=∠G．∴AB=BG．

    在△ADE和△GCE中，∵∠DAE=∠G，∠AED=∠GEC，DE=EC，

    ∴△ADE≌△GCE，∴AD=CG．

    ∵AB=BC+CG，∴AB=BC+AD．

    反思  本题采用“补短”的方法解决线段和的问题，这是证明线段和差问题的常用方法，即把短线段BC补一段CG，使CG=AD，这样问题就转化成证明BG=AB．本题也可以用“截长法”来处理，过点E作AB的垂线段，即把长线段AB截成两段，证明其中一段等于AD，再证余下的一段等于BC．同学们不妨试一试．