1.4 全等三角形 同步练习

    【知识提要】

    1．会说出怎样的两个图形是全等图形，并会用符号语言表示两个三角形全等．

    2．知道全等三角形的有关概念，会在全等三角形中正确找出对应顶点、对应边、对应角．

    3．会说出对应边、对应角相等的性质．

    【学法指导】

    1．两个三角形的全等是指两个图形之间的一种对应关系，对应关系是按一定标准的一对一的关系，“互相重合”是判断其对应部分的标准．

    2．实际遇到的图形，两个全等三角形并不重合在一起，但其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法得到的．

    范例积累

【例1】  如图，△ABD≌△CDB，且AB、CD是对应边，下面四个结论中不正确的是（  ）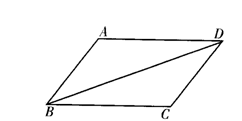

    A．△ABD和△CDB的面积相等

    B．△ABD和△CDB的周长相等

    C．∠A+∠ABD=∠C+∠CBD

    D．AD∥BC且AD=BC

    【分析】  由于两个三角形完全重合，故面积周长相等，对应角对应边相等，而∠ABD与∠CBD不是对应角，所以C符号题意．

    【解】  选C．

【例1】            如图，已知△ABC≌△ADE，试找出对应边、对应角．

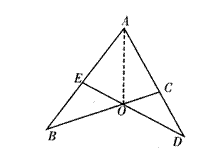    【分析】  连结AO，将△ABC沿AO翻折180°，即可得到△ADE，对应元素易找，找对应元素常利用“运动法”来找．

    a．翻折法：找到中心线，经此翻折后能互相重合的两个三角形，易发现其对应元素．