|
1.5 三角形全等的条件(一)同步练习
【知识提要】
1.掌握已知三边画三角形的方法.
2.掌握边边边公理,能用边边边公理说明两个三角形全等.
3.了解三角形的稳定性.
【学法指导】
1.在公理形成过程中学会实验、观察、归纳.
2.通过几何说明养成尊重客观事实、形成质疑的习惯.
范例积累
【例1】 下列判断,其中正确的是( )
A.三个角对应相等的两个三角形全等
B.周长相等的两个三角形全等
C.周长相等的两个等边三角形全等
D.有两边和第三边上的高对应相等的两个三角形全等
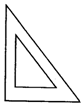
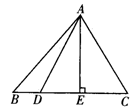
【分析】 A不正确,如图1,两个三角形,三内角分别为30°,60°,90°,显然不全等;B不正确,如两个三角形周长都是60,一个三角形的三边长为20、20、20,另一个三角形三边长为15、20、25,显然不全等;C正确,D如图2,AB=AB、AC=AD,第三边上的高AE相同,显然不全等,故D不正确.
(1) (2)
【解】选C.
【例1】 如图,已知AB=AC,AE=AD,BD=CE,说出∠1=∠2成立的理由. 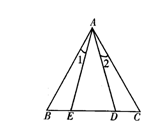 【分析】 利用全等三角形对应边相等,对应角相等是证明线段或角相等的重要方法,要善于从组 【分析】 利用全等三角形对应边相等,对应角相等是证明线段或角相等的重要方法,要善于从组 |

