|
6.3 用乘法公式分解因式(一)
【知识提要】
1.掌握平方差公式:a2-b2=(a+b)(a-b).
2.运用平方差公式因式分解.
【学法指导】
1.公式左边的多项式形式上是二项式,且两项的符号相反.
2.公式左边的每一项都可以化为某数或某式的平方形式.
3.公式左边分解的结果是这两个数或两个式子的和与它们的差的积.
4.公式中的a、b既可以表示单独的数或字母,也可以表示一个单项式或多项式.
范例积累
【例1】 分解因式:
(1)a2-4b2; (2)-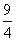 x2+ x2+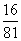 y2. y2.
【分析】 本题两小题都是二次式,这两项符号恰好相反,它们都能写成某数平方的形式,这符合平方差公式的特征.
【解】 (1)a2-4b2=a2-(2b)2=(a+2b)(a-2b);
(2)解法(一):-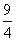 x2+ x2+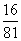 y2=-(- y2=-(-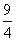 x2- x2-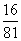 y2)=-[( y2)=-[(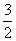 x)2-( x)2-(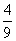 y)2] y)2]
=-(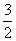 x+ x+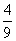 y)( y)(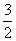 x- x-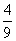 y) y)
解法(二):-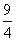 x2- x2-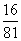 y2 y2
=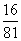 y2- y2-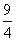 x2=( x2=(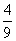 y)2-( y)2-(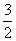 x)2=( x)2=(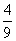 y+ y+ x)( x)(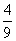 y- y- x). x). 【注意】 第(1)题相当于公式中a是a,b是2b,这种套用的过程其实蕴含了“换元”思想.第(2)小题 |

