|
第3课时 函数的单调性
一、单调性
1.定义:如果函数y=f (x)对于属于定义域I内某个区间上的任意两个自变量的值x1、、x2,当x1、<x2时,①都有 ,则称f (x)在这个区间上是增函数,而这个区间称函数的一个 ;②都有 ,则称f (x)在这个区间上是减函数,而这个区间称函数的一个 .
若函数f(x)在整个定义域l内只有唯一的一个单调区间,则f(x)称为 .
2.判断单调性的方法:
(1) 定义法,其步骤为:① ;② ;③ .
(2) 导数法,若函数y=f (x)在定义域内的某个区间上可导,①若 ,则f (x)在这个区间上是增函数;②若 ,则f (x)在这个区间上是减函数.
二、单调性的有关结论
1.若f (x), g(x)均为增(减)函数,则f (x)+g(x) 函数;
2.若f (x)为增(减)函数,则-f (x)为 ;
3.互为反函数的两个函数有 的单调性;
4.复合函数y=f [g(x)]是定义在M上的函数,若f (x)与g(x)的单调相同,则f [g(x)]为 ,若f (x), g(x)的单调性相反,则f [g(x)]为 .
5.奇函数在其对称区间上的单调性 ,偶函数在其对称区间上的单调性 .
例1. 已知函数f(x)=ax+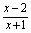 (a>1),证明:函数f(x)在(-1,+∞)上为增函数. (a>1),证明:函数f(x)在(-1,+∞)上为增函数.
证明 方法一 任取x1,x2∈(-1,+∞),
不妨设x1<x2,则x2-x1>0, 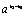 >1且 >1且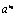 >0, >0,
∴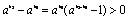 ,又∵x1+1>0,x2+1>0, ,又∵x1+1>0,x2+1>0,
∴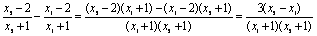 >0, >0,
于是f(x2)-f(x1)=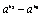 + +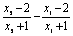 >0, >0,
故函数f(x)在(-1,+∞)上为增函数.
方法二 f(x)=ax+1-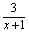 (a>1), (a>1), 求导数得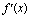 =axln =axln |

