|
1.2.1任意角的三角函数
教学目的:
1、 掌握任意角的正弦、余弦、正切的定义,了解任意角的余切、正割、余割的定义;
2、 掌握三角函数值的符号的确定方法;
3、 记住三角函数的定义域、值域,诱导公式(一);
4、利用三角函数线表示正弦、余弦、正切的三角函数值。
教学重点、难点
重点:三角函数的定义,各三角函数值在每个象限的符号,特殊角的三角函数值
难点:对三角函数的自变量的多值性的理解,三角函数的求值中符号的确定
教学过程:
一、复习引入:
初中锐角的三角函数是如何定义的?
在Rt△ABC中,设A对边为a,B对边为b,C对边为c,锐角A的正弦、余弦、正切依次为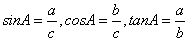 . .
角推广后,这样的三角函数的定义不再适用,我们必须对三角函数重新定义。
二、讲授新课:
1.三角函数定义
在直角坐标系中,设α是一个任意角,α终边上任意一点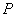 (除了原点)的坐标为 (除了原点)的坐标为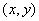 ,它与原点的距离为 ,它与原点的距离为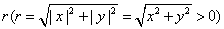 ,那么 ,那么
(1)比值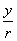 叫做α的正弦,记作 叫做α的正弦,记作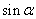 ,即 ,即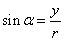 ; ;
(2)比值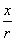 叫做α的余弦,记作 叫做α的余弦,记作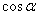 ,即 ,即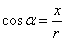 ; ;
(3)比值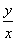 叫做α的正切,记作 叫做α的正切,记作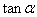 ,即 ,即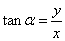 ; ;
说明:①α的始边与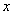 轴的非负半轴重合,α的终边没有表明α一定是正角或负角,以及α 轴的非负半轴重合,α的终边没有表明α一定是正角或负角,以及α
的大小,只表明与α的终边相同的角所在的位置;
②根据相似三角形的知识,对于确定的角α,六个比值不以点 在α的终边上的位置的改变而改变大小; 在α的终边上的位置的改变而改变大小;
③当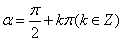 时,α的终边在 时,α的终边在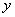 轴上,终边上任意一点的横坐标 轴上,终边上任意一点的横坐标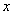 都等于 都等于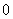 ,所以 ,所以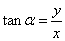 无意义; 无意义; |

