|
一、
sin(360°k+a) = sina, cos(360°k+a) =cosa.
tan(360°k+a) = tga, cot(360°k+a) = ctga.
sec(360°k+a) = seca, csc(360°k+a) = csca | |
1.公式1:(复习)
2.对于任一0°到360°的角,有四种可能(其中a为不大于90°的非负角)
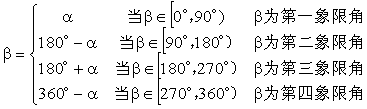 (以下设a为任意角) (以下设a为任意角)
3.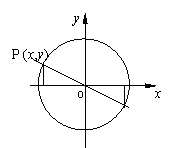 公式2: 公式2:
设a的终边与单位圆交于点P(x,y),则180°+a终边与单位圆交于点P’(-x,-y)
sin(180°+a) = -sina, cos(180°+a) = -cosa.
tan(180°+a) = tga, cot(180°+a) = ctga.
sec(180°+a) = -seca, csc(180°+a) = -csca
4.公式3:
如图:在单位圆中作出与角的终边,同样可得:
 sin(-a) = -sina, cos(-a) = cosa. sin(-a) = -sina, cos(-a) = cosa.
tan(-a) = -tana, cot(-a) = -cota.
sec(-a) = seca, csc(-a) = -csca
5.公式4: sin(180°-a) = sin[180°+(-a)] = -sin(-a) = sina,
cos(180°-a) = cos[180°+(-a)] = -cos(-a) = -cosa,

同理可得: sin(180°-a) = sina, cos(180°-a) = -cosa.
tan(180°-a) = -tana, cot(180°-a) = -cota.
sec(180°-a) = -seca, csc(180°-a) = csca
 6.公式5: sin(360°-a) = -sina, cos(360°-a) = cosa. 6.公式5: sin(360°-a) = -sina, cos(360°-a) = cosa.
tan(360°-a) = -tana, cot(360°-a) = -cota.
sec(360°-a) = seca, csc(360°-a) = -csca
三、小结:360° k + a, 180° - a, 180° + a, 360° - a, - a的三角函数值等于a的同名三角函数值再加上一个把a看成锐角时原函数值的符号
四、例题:P29—30 例一、例二、例三
P31—32 例四、例五、例六 略
五、作业:P30 练习
P32 练习
P33 习题4.5
| 
