|
第1课时 向量的概念与几何运算
1.向量的有关概念
⑴ 既有 又有 的量叫向量.
的向量叫零向量. 的向量,叫单位向量.
⑵ 叫平行向量,也叫共线向量.规定零向量与任一向量 .
⑶ 且 的向量叫相等向量.
2.向量的加法与减法
⑴ 求两个向量的和的运算,叫向量的加法.向量加法按 法则或 法则进行.加法满足 律和 律.
⑵ 求两个向量差的运算,叫向量的减法.作法是将两向量的 重合,连结两向量的 ,方向指向 .
3.实数与向量的积
⑴ 实数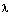 与向量 与向量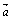 的积是一个向量,记作 的积是一个向量,记作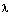 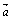 .它的长度与方向规定如下: .它的长度与方向规定如下:
① | 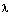 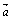 |= . |= .
② 当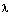 >0时, >0时,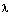 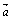 的方向与 的方向与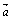 的方向 ; 的方向 ;
当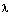 <0时, <0时,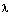 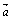 的方向与 的方向与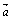 的方向 ; 的方向 ;
当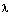 =0时, =0时,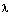 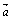 . .
⑵ 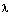 (μ (μ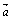 )= . )= .
(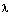 +μ) +μ)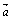 = . = .
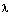 ( (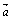 + +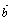 )= . )= .
⑶ 共线定理:向量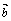 与非零向量 与非零向量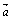 共线的充要条件是有且只有一个实数λ使得 . 共线的充要条件是有且只有一个实数λ使得 .
4.⑴ 平面向量基本定理:如果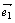 、 、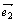 是同一平面内的两个不共线的向量,那么对于这一平面内的任一向量 是同一平面内的两个不共线的向量,那么对于这一平面内的任一向量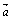 ,有且只有一对实数 ,有且只有一对实数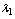 、 、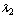 ,使得 . ,使得 . ⑵ 设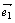 、 、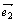 是一组基 是一组基 |

