|
复习旧知识
例题选讲
练习
引出数乘向量
例题选讲
巩固练习
小结
作业
|
(1)向量加法运算法则
几何中向量加法是用几何作图来定义的,一般有两种方法,即向量加法的三角形法则(“首尾相接,首尾连”)和平行四边形法则(对于两个向量共线不适应)
(2)加法的运算律:
向量加法的交换律: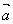 + +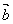 = =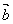 + +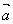
向量加法的结合律:(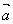 + +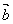 ) + ) +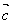 = =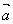 + ( + (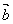 + +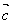 ) )
(3)向量减法法则:向量a加上的b相反向量,叫做a与b的差 即:a - b = a + (-b) 即:a - b = a + (-b)
即a - b可以表示为从向量b的终点指向向量a的终点的向量
例题1: 用向量方法证明:对角线互相平行的四边形是平行四边形。
已知: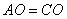 , ,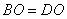 ,求证:四边形 ,求证:四边形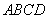 是平行四边形。 是平行四边形。
证明:设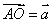 , ,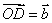 ,则 ,则 , ,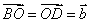
∴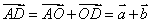 , ,
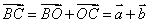
∴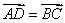 ,又∵点 ,又∵点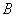 不在 不在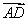
∴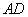 平行且等于 平行且等于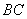
所以,四边形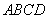 是平行四边形. 是平行四边形.
例题2:(选讲)试证:对任意向量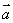 , ,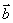 都有 都有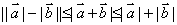 . .
证明:(1)当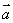 , ,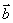 中有零向量时,显然成立。 中有零向量时,显然成立。
(2)当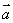 , ,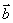 均不为零向量时: 均不为零向量时:
①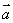 , ,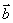 ,即 ,即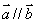 时,当 时,当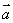 , ,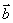 同向时, 同向时,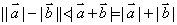 ; ;
当,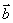 异向时, 异向时, . .
②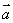 , ,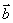 不共线时,在 不共线时,在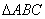 中, 中,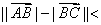 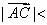 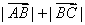 , ,
则有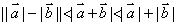 . .
∴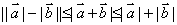 其中: 其中:
当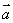 , ,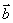 同向时, 同向时,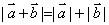 , ,
当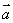 , ,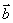 同向时, 同向时,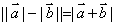 . .
练习:已知非零向量 ,作出 ,作出 + + + + 和(- 和(- )+(- )+(- )+(- )+(- ) )
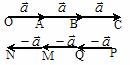
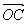 = =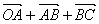 = = + + + + =3 =3
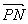 = =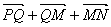 =(- =(- )+(- )+(- )+(- )+(- )=-3 )=-3
(1)3 与 与 方向相同且|3 方向相同且|3 |=3| |=3| |;(2)-3 |;(2)-3 与 与 方向相反且|-3 方向相反且|-3 |=3| |=3| | |
定义:实数与向量的积:实数λ与向量 的积是一个向量,记作:λ 的积是一个向量,记作:λ
(1)|λ |=|λ|| |=|λ|| | |
(2)λ>0时λ 与 与 方向相同;λ<0时λ 方向相同;λ<0时λ 与 与 方向相反;λ=0时λ 方向相反;λ=0时λ = =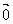
数乘向量运算定律
结合律:λ(μ )=(λμ) )=(λμ) ① ①
第一分配律:(λ+μ) =λ =λ +μ +μ ② ②
第二分配律:λ( + +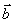 )=λ )=λ +λ +λ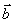 ③ ③
例题3:计算:(1)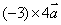 ; ;
(2)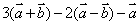 ; ;
(3)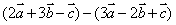 . .
解:(1)原式=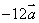 ; (2)原式= ; (2)原式=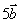 ; ;
(3)原式=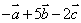 . .
例题4:若3m+2n=a,m-3n=b,其中a,b是已知向量,求m,n.
分析:此题可把已知条件看作向量m、n的方程,通过方程组的求解获得m、n.
解:记3m+2n=a ① m-3n=b ②
3×②得3m-9n=3b ③
①-③得11n=a-3b. ∴n=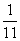 a- a-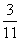 b ④ b ④
将④代入②有:m=b+3n=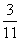 a+ a+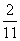 b b
评述:在此题求解过程中,利用了实数与向量的积以及它所满足的交换律、结合律,从而解向量的二元一次方程组的方法与解实数的二元一次方程组的方法一致.
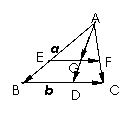
1.如图,在△ABC中,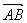 = = , , 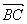 = =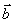 ,AD为边BC的中线,G为△ABC的重心,求向量 ,AD为边BC的中线,G为△ABC的重心,求向量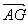
 解法一:∵=, = 则== 解法一:∵=, = 则==
∴=+=+而=
∴=+
解法二:过G作BC的平行线,交AB、AC于E、F
∵△AEF∽△ABC,
== == 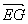 = =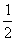 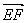 = =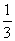 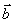
∴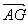 = =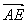 + +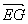 = =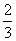  + +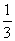 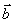
实数与向量的积的定义可以看作是数与数的积的概念的推广.启发学生在掌握向量加法的基础上,学习实数与向量的积的概念及运算律,引导学生从特殊归纳到一般.
在学习实数与向量的积的运算律时,应启发学生寻求其与代数运算中实数乘法的运算律的相似性,但应注意它们之间的区别,从而掌握实数与向量的积及其应用.
书89页A 组2,3
B 组1
补充:在   ABCD中,设对角线 ABCD中,设对角线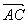 = = , ,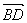 = =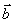 试用 试用 , , 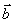 表示 表示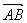 , ,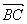
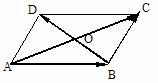 解法一: 解法一: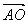 = =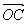 = =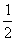  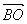 = =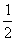 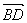 = =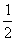 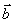
∴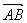 = =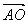 + +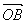 = =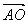 - -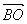 = =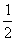  - -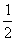 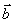
 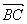 = =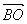 + +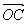 = =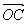 + +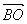 = =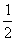  + +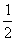 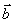
解二:设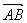 = =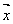 , ,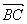 = =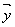
 则 则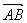 + +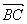 = =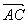 ,即 ,即 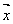 + +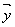 = = ; ;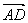 - -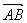 = =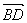 ,即 ,即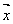 - -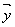 = =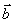
∴ 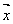 = =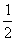 ( ( - -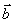 ), ), 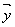 = =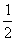 ( ( + +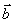 ) )
即 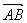 = =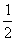 ( ( - -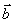 ) ) 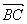 = =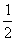 ( ( + +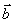 ) )
|
教师提出问题学生认真思考后回答
通过例题进一步体会向量加法与减法的运算法则,以及运算律的使用
利用练习找出三种运算的关系,引出数乘运算
引导学生探究、验证运算律(3),教师投影展示学生的验证结果,说明运算律的合理性,让学生总结运算规律.
教师适当点拨,学生通过交流完成
启发学生将所学的三种运算结合起来解决问题
分层次留作业,学生分层完成 |
通过对旧知识的复习,使得学生能够对旧知识形成更加深刻地印象。
通过学生练习,由向量加法得出数乘向量的公式和运算律,并且比较记忆
学生独立完成巩固运算律,检验定义的使用,让学生体验成功.
对教材的知识适当深化有利于提高学生的认知水平
通过适当的练习熟练掌握运算法则及运算律
|

