|
§2.2.3向量的数乘运算及其几何意义(新教改A版教材)
教学目标:(1)掌握向量数乘运算法则,并理解其几何意义;
(2)让学生能由实数运算律类比向量运算律,并且验证强化对知识的形成过程的认识,正确表示结果;
(3)初步学会用向量的方法解决几何问题和实际应用问题。
教学重点、难点:
重点:向量的数乘运算法则的理解及几何意义。
难点:正确运用法则解决几何问题。
教学过程:
|
教学
环节 |
教学内容 |
师生互动 |
设计意图 |
|
复习
提问
复习提问 |
(1)前两节我们介绍了解了向量的加法和减法,其中“加法”我们要牢固掌握“三角形法则”和“平行四边形法则”;
  例如:平面内有向量 例如:平面内有向量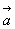 和 和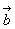 ,: 和 ,: 和
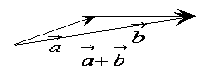 ①当顺次首尾连结时: ,和向量即为图中所示;(副板书) ①当顺次首尾连结时: ,和向量即为图中所示;(副板书)
②当重合起点或终点时,图略,和向量应用“平行四边形法则”求得;
而且向量的减法我们可以看成一个向量加上另一个向量的等模、反向、或记住口诀“连结终点,指向被减”直接由代数形式求得结果。
例如: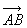 - -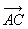 = =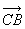
(2)下面我们来看这么一道题:
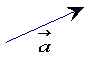 1.例:已知如图向量 1.例:已知如图向量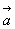 为非零向量,试用作图方式表示 为非零向量,试用作图方式表示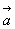 + +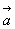 + +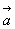 和- 和-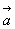 +(- +(-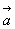 ) )
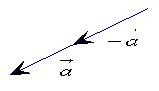 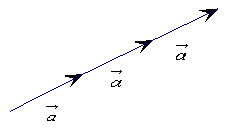 (投影) (投影)
|
师生互答
与
教师讲解
结合
师生互答
与
教师讲解
结合 |
复习旧知识,
引出新知识
复习旧知识
引出新知识 | |

