|
2.4《等比数列》教案
天津市武清区大良中学 孙彦强
一、能力要求:
1、掌握等比数列的概念,等比中项的概念,能利用定义判定等比数列;
2、理解等比数列的通向公式及推导,并能简单的应用公式;
3、了解等比数列的通向公式与指数函数的关系。
二、教学重点、难点:
重点: 等比数列的概念和通向公式及其推导;等比数列通向公式的应用。
难点:等比数列通向公式的应用。
三、预习问题处理:
1、等比数列的概念:一般的, ,那么这个数列叫做等比数列,这个常数叫做等比数列的 ,公比通常用字母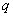 表示。 表示。
2、若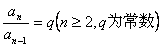 ,则称数列 ,则称数列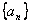 为 , 为 ,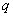 为 ,且 为 ,且 。 。
3、若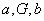 成等比数列,则 ;其中 成等比数列,则 ;其中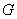 叫做 叫做 与 与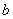 的 。此时 的 。此时 与 与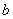 (填同号或异号)。 (填同号或异号)。
4、等比数列的通项公式为: 。
5、首项为正数的等比数列的公比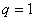 时,数列为 数列;当 时,数列为 数列;当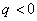 时,数列为 数列;当 时,数列为 数列;当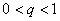 时,数列为 数列;当 时,数列为 数列;当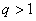 时,数列为 数列。 时,数列为 数列。
6、判断正误:
①1,2,4,8,16是等比数列; ( )
②数列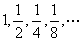 是公比为2的等比数列; ( ) 是公比为2的等比数列; ( )
③若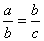 ,则 ,则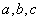 成等比数列; ( ) 成等比数列; ( )
④若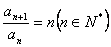 ,则数列 ,则数列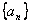 成等比数列; ( ) 成等比数列; ( )
7、思考:如何证明一个数列是等比数列。
|

