|
2.2.2 二次函数的性质与图象 学案
【预习要点及要求】
1.二次函数的一般方法——配方法。
2.二次函数的图像的画法。
3.二次函数的图像的顶点坐标、对称轴方程、单调区间和最值的求法。
4.掌握研究二次函数图像和性质的配方法。
5.进一步掌握二次函数的图像和性质。
6.会综合运用二次函数图像和性质解决有关问题。
【知识再现】
1. 二次函数的一般形式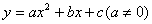
2.二次函数的顶点坐标(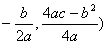
【概念探究】
阅读课本57页到例1的上方,完成下列问题
1、二次函数的定义及图象的形状是怎样的?
2、函数_____________________叫二次函数,它的定义域是_________________.
3、当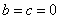 时,二次函数 时,二次函数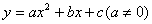 变为___________,它的图像和性质特征为:(1)顶点坐标________,奇偶性为_______,图形关于_______对称; 变为___________,它的图像和性质特征为:(1)顶点坐标________,奇偶性为_______,图形关于_______对称;
(2)当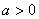 时,抛物线的开口______,在_________上是增函数,在_________上是减函数,当x=_____有最小值_______;当 时,抛物线的开口______,在_________上是增函数,在_________上是减函数,当x=_____有最小值_______;当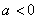 时,抛物线的开口_______,在_________上是增函数,在____________上是减函数,当x=______有最大值_______. 时,抛物线的开口_______,在_________上是增函数,在____________上是减函数,当x=______有最大值_______.
(3) 当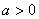 时,抛物线在x轴的______,开口向上并随 时,抛物线在x轴的______,开口向上并随 的增大逐渐______;当 的增大逐渐______;当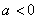 时,抛物线在x轴的______,开口向下并随 时,抛物线在x轴的______,开口向下并随 的增大逐渐______; 的增大逐渐______;
【例题解析】
例1、求函数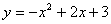 的顶点坐标,对称轴以及函数的单调区间. 的顶点坐标,对称轴以及函数的单调区间.
例2、求函数 |

