|
2.2.2 二次函数的性质与图象 教案
【教学目标】
1、 让学生学会画函数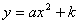 的图象,并能通过图象和解析式,正确地说出开口方向,对称轴以及顶点坐标,图象性质. 的图象,并能通过图象和解析式,正确地说出开口方向,对称轴以及顶点坐标,图象性质.
2、 通过探索让学生经历二次函数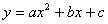 性质探究的过程,理解二次函数 性质探究的过程,理解二次函数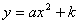 的性质及它与函数 的性质及它与函数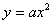 的关系。 的关系。
3、在教学中渗透美的教育,渗透数形结合的思想.
重点:理解二次函数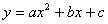 的性质, 的性质,
难点:二次函数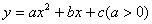 的增区间和减区间。 的增区间和减区间。
【概念探究】
1、二次函数的定义及图象的形状是怎样的?
2、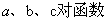 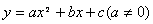 的性质与图象有哪些影响? 的性质与图象有哪些影响?
3、分析二次函数的性质时,需要对其解析式进项变形,主要用什么方法?
4、基本知识填空:
(1)、函数_____________________叫二次函数,它的定义域是_________________.
(2)、若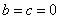 时,二次函数 时,二次函数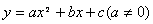 是一条____________的抛物线, 是一条____________的抛物线,
(3)、二次函数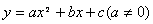 的顶点坐标为_______________,对称轴为_______;当 的顶点坐标为_______________,对称轴为_______;当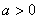 时,抛物线的开口_____________,在________________上是增函数,在____________ 时,抛物线的开口_____________,在________________上是增函数,在____________
上是减函数;当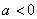 时,抛物线的开口_____________,在________________上是增函数,在____________ 时,抛物线的开口_____________,在________________上是增函数,在____________
上是减函数.
【例题解析】
例1、已知关于x的不等式k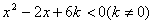
(1)若不等式的解集为{x|x<-3或x>-2},求k的值;
(2)若不等式的解集为R,求k的值; |

