|
1.2.4(第一课时) 诱导公式
教学目标:
1. 借助单位圆的直观性探索正弦、余弦、正切的诱导公式,并掌握其应用;
2. 经历由几何特征发现数量关系的学习过程,培养数形结合的分析问题能力;通过独立探讨公式,培养抽象概括能力;了解对称变换思想在研究数学问题中的应用,初步形成用对称变换思想思考问题的习惯。
3. 揭示事物间的普遍联系规律,培养辨证唯物主义思想
教学重点:诱导公式(一)、(二)的探究、推导及利用诱导公式进行简单的三角函数式的求值、化简和恒等式的证明。
教学难点:在单位圆中对所讨论角与a角终边位置关系特点发现对称性提出研究方法
教学方法与学习指导策略建议
这一部分知识的学习,建议主要以师生互动为主。多给学生一些感性认识,通过讨论、辨析获得对知识更深层次的理解。
教学过程:
|
教学
环节 |
教学内容 |
师生互动 |
设计意图 |
|
复
习
引
入
|
复习三角函数的定义、单位圆与三角函数线
直角坐标系中,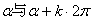 的终边相同,由三角函数的定义,它们的三角函数值相等,即公式(一): 的终边相同,由三角函数的定义,它们的三角函数值相等,即公式(一):
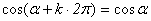
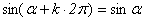
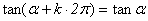
指出结构特征和作用:
这组公式可以统一概括为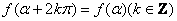 的形式,其特征是:等号两边是同名函数,且符号都为正 的形式,其特征是:等号两边是同名函数,且符号都为正
由这组公式还可以看出,三角函数是“多对一”的单值对应关系,明确了这一点,为今后学习函数的周期性打下基础
诱导公式(一)的作用:把任意角的正弦、余弦、正切化为0º―360º之间角的正弦、余弦、正切
例1 求下列各三角函数值:
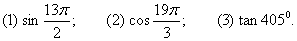
|
教师运用多媒体展示三角函数的定义、单位圆与三角函数线
共同探讨公式(一)的结构特征和作用
由教师提问,学生相互交流,教师纠正、完善。
由学生完成
如何求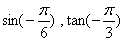 的三角函数值呢? 的三角函数值呢? |
共同回顾,为新课做准备。
理性地把握公式
体会诱导公式的作用。
将问题一般化,转化为探索 与 与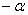 的三角函数间关系 的三角函数间关系 | |

