|
1.2.4 诱导公式(一)
一、学习目标
1.通过本节内容的教学,使学生掌握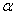 + +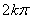 ,- ,-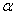 角的正弦、余弦和正切的诱导公式及其探求思路,并能正确地运用这些公式进行任意角的正弦、余弦和正切值的求解、简单三角函数式的化简与三角恒等式的证明; 角的正弦、余弦和正切的诱导公式及其探求思路,并能正确地运用这些公式进行任意角的正弦、余弦和正切值的求解、简单三角函数式的化简与三角恒等式的证明;
2.通过公式的应用,培养学生的化归思想,以及信息加工能力、运算推理能力、分析问题和解决问题的能力;
二、教学重点、难点
重点:四组诱导公式及这四组诱导公式的综合运用.
难点:公式(四)的推导和对称变换思想在学生学习过程中的渗透.
三、教学方法
先由学生自学,然后由教师设置一些问题供学生思考,在此基础上,可以通过讲授再现概念,通过练习理解概念,完成教学.
四、教学过程
|
教学环节 |
教学内容 |
师生互动 |
设计意图 |
|
复习引入 |
1、 初中我们已经会求锐角的三角函数值。
2、 和30°、45°、60°终边相同的角如何表示?
本节我们将研究任意角三角函数值之间的某中关系,以及如何求任意角的三角函数值。 |
教师提问:0°、30°、45°、60°、90°的正弦、余弦、正切的三角函数值是多少?
学生回答
我们如何求360°、390°、-315°的三角函数值呢? |
温故知新 |
|
公式导入 |
1.公式(一)
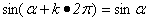
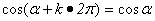 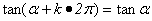
(其中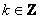 ) )
诱导公式(一)的作用:把把绝对值大于360º的任意角的正弦、余弦、正切的三角函数问题转化为绝对值小于360º角的正弦、余弦、正切三角函数问题,其方法是先在绝对值小于360º角找出与角 终边相同的角,再把它写成诱导公式(一)的形式,然后得出结果 终边相同的角,再把它写成诱导公式(一)的形式,然后得出结果
2.公式(二):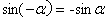
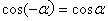
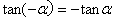
它说明角-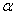 与角 与角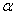 的正弦值互为相反数,而它们的余弦值相等.这是因为,若没 的正弦值互为相反数,而它们的余弦值相等.这是因为,若没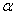 的终边与单位圆交于点P(x,y),则角- 的终边与单位圆交于点P(x,y),则角-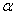 的终边与单位圆的交点必为P´(x,-y)(如图4-5-2).由正弦函数、余弦函数的定义,即可得 的终边与单位圆的交点必为P´(x,-y)(如图4-5-2).由正弦函数、余弦函数的定义,即可得
sin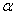 =y, cos =y, cos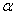 =x, =x,
sin(-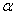 )=-y, cos(- )=-y, cos(-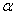 )=x, )=x,
所以:sin(-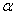 )= -sin )= -sin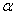 , cos(- , cos(-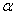 )= cosα )= cosα
公式二的获得主要借助于单位圆及正弦函数、余弦函数的定义.根据点P的坐标准确地确定点P´的坐标是关键,这里充分利用了对称性质.事实上,在图1,点P´与点P关于x轴对称.直观的对称形象为我们准确写出P´的坐标铺平了道路,体现了数形结合这一数学思想的优越性.
公式(三)
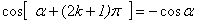
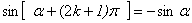
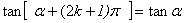
由公式(一)可以看出,角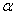 和 和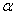 加上 加上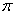 偶数倍的所有三角函数值相等。角 偶数倍的所有三角函数值相等。角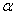 和 和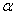 加上 加上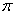 奇数倍的正,余弦值互为相反数; 角 奇数倍的正,余弦值互为相反数; 角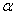 和 和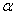 加上 加上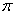 奇数倍的正切函数值相等。 奇数倍的正切函数值相等。
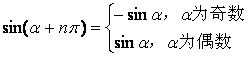 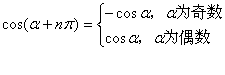 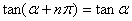
|
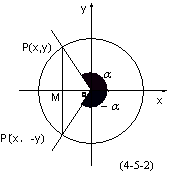
让学生在单位圆中画出α角与-α角,观察两个角的位置关系。
引导学生在单位圆中画出α角与π+α角,观察其位置关系,在结合公式(一)得到公式(三)

|
1.根据任意角的三角函数定义可知两个角若终边相同,那么它们的三角函数值也应该相同。由此导出公式(一)
2.学生在单位圆中画出α角与-α角,观察出角的终边关于x轴对称,结合三角函数定义可得到公式(二)
3.利用角的终边在单位圆中的不同位置关系而得到相应的诱导公式。 | |

