|
2.4.1 向量在平面几何中的应用
一、教学目标
1.知识与技能:
运用向量的有关知识(向量加减法与向量数量积的运算法则等)解决平面几何和解析几何中直线或线段的平行、垂直、相等、夹角和距离等问题
2.过程与方法:
通过应用举例,让学生会用平面向量知识解决几何问题的两种方法-----向量法和坐标法
3.情感、态度与价值观:
通过本节的学习,让学生体验向量在解决几何问题中的工具作用,增强学生的积极主动的探究意识,培养创新精神。
二、教学重点难点
重点:理解并能灵活运用向量加减法与向量数量积的法则解决几何问题.
难点:选择适当的方法,将几何问题转化为向量问题加以解决.
三、教学方法
本小节主要是例题教学,要让学生体会思路的形成过程,体会数学思想方法的应用。教学中,教师创设问题情境,引导学生发现解题方法,展示思路的形成过程,总结解题规律。指导学生搞好解题后的反思,从而提高学生综合应用知识分析和解决问题的能力。
四、教学内容安排:
|
教学
环节 |
教学内容 |
师生互动 |
设计意图 |
|
复
习
准
备 |
课前复习任务(由学生总结成书面材料)
(1)向量的线性运算是怎样的?
(2)平面向量共线的含义及条件是什么?
(3)平面向量的基本定理及向量的坐标运算有哪些?
(4)平面向量的数量积中有哪些主要内容?
|
讨论:
(1)若O为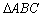 重心,则 重心,则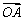 + +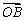 + +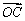 = =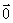
(2)水渠横断面是四边形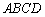 , ,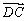 = =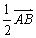 ,且 ,且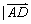 |= |=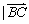 |,则这个四边形为等腰梯形.类比几何元素之间的关系,你会想到向量运算之间都有什么关系? |,则这个四边形为等腰梯形.类比几何元素之间的关系,你会想到向量运算之间都有什么关系?
|
让学生回顾学过的知识有力于本节课的进行 |
|
新
课
引
入 |
平移、全等、相似、长度、夹角等几何性质可以由向量线性运算及数量积表示出来: 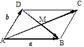 例如,向量数量积对应着几何中的长度.如图: 平行四边行 例如,向量数量积对应着几何中的长度.如图: 平行四边行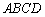 中,设 中,设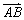 = =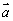 , ,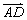 = =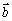 ,则 ,则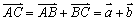 (平移), (平移),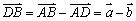 , ,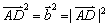 (长度).向量 (长度).向量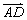 , ,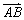 的夹角为 的夹角为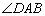
|
讨论(让学生回顾学过的知识,有利于本课的顺利进行):(1)向量运算与几何中的结论"若 ,则 ,则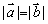 ,且 ,且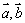 所在直线平行或重合"相类比,你有什么体会?(2)由学生举出几个具有线性运算的几何实例.(3)向量平行、垂直的判定方法 所在直线平行或重合"相类比,你有什么体会?(2)由学生举出几个具有线性运算的几何实例.(3)向量平行、垂直的判定方法
|
让学生掌握用向量方法解平面几何问题的步骤:
建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量.
通过向量运算研究几何运算之间的关系,如距离、夹角等.
把运算结果"翻译"成几何关系.
| |

