|
三、教学内容安排
1.复习引入,
首先提出下列思考问题:回顾用向量法解决平面几何问题的基本思维过程(三步曲),为学习用向量法解决物理及生活中的问题,奠定理论和方法的基础;
2.回顾情景,观察思考,探索思路
然后,再就课前预习作业:情景1、情景2得体会,针对情景3为例,引导学生从数学的角度解释这些现象。(即:首先在探讨用向量知识表示物理量的前提下,再利用数学中向量的线性关系表示问题所涉及到的物理量(矢量)之间的关系(这里不妨设)
情景1:两个同学共同提一较重的物体(一个旅行包,一筒水,一摞书等)。两位同学手臂间的夹角的变化与两人用力大小变化间的关系(体会夹角越大越省力)
情景2:在单杠上做引体向上运动(同上)
情景3:教具演示:
详见《参考样例》P22
3.启发联想、拓展思维
详见《参考样例》P22
4.深化练习、总结规律
问题1详见《参考样例》P22
问题2详见《参考样例》P22
由于课本中的例题,对一部分学习能力强的同学可能会觉得课堂密度不够(新高一一开学,物理就讲力学。所以到了数学讲向量时,数学书上地例题就显得太简单了)
补充问题3:模块:物理1
第一章 运动的描述(高一 上学期 第一学段)
第二节 时间和位移
位移的概念是学生学习高中物理遇到的第一个矢量,这个阶段由于初步接触矢量,所以主要解决一条直线上的矢量运算中的减法,位移:即初位置到末位置的有向线段,物理课本上,先介绍位置,位置用坐标系中的坐标表示(本节主要是一维问题),位移就定义为:坐标的差值。规定正方向之后,用“+”“-”号表示位移的方向。
第三节 运动快慢的描述——速度
速度:是矢量,但是此时还不涉及其运算问题,只是让学生知道:速度是矢量;
第五节 速度变化快慢的描述——加速度
加速度:是矢量,但是此时仍不涉及其运算问题,只是让学生知道:加速度也是矢量;
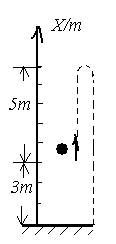 实例1:从高出地面3m的位置竖直向上抛出一个小球,它上升5m后回落,最后到达地面(如图)。分别以地面和抛出点为原点建立坐标系,方向均以向上为正,填写以下表格。 实例1:从高出地面3m的位置竖直向上抛出一个小球,它上升5m后回落,最后到达地面(如图)。分别以地面和抛出点为原点建立坐标系,方向均以向上为正,填写以下表格。
|
坐标原点的设置 |
出发点的坐标 |
最高点的坐标 |
落地点的坐标 |
上升过程的位移 |
下落过程的位移 |
全过程的总位移 |
|
以地面为原点 |
|
|
|
|
|
|
|
以抛出点为原点 |
|
|
|
|
|
|
分析:根据题目要求,画出示意图。

得结果如下表:
|
坐标原点位置 |
出发点坐标 |
落地点坐标 |
上升过程中的位移(m) |
下落过程中的位移(m) |
全过程总位移
(m) |
|
以地面为原点 |
3 |
8 |
5m |
-8m |
-3m |
|
以抛出点为原点 |
0 |
-3 |
5m |
-8m |
-3m |
补充问题4:
第四章 牛顿运动定律(高一 上学期 第一学段)
例题:一个滑雪人,质量m=75kg,以v0=2m/s的初速度沿山坡匀加速下滑,山坡的倾角q=300,在t=5s时间内滑下的路程为X=60m,求:滑雪人受到的阻力(包括摩擦和空气阻力,重力加速度g的值取10)
分析:由于要求滑雪者所受的f, 首先对其进行受力分析:由于f与支持力N和重力G不共线且N的大小不知,所以利用平衡条件,采用正交分解法,以f所在直线为x轴,垂直于f,即N所在直线为y轴建立平面直角坐标系,将G分解为x、y轴方向。
由平衡条件可布列方程组。解法如下:
解:如图,受力分析:重力G,支持力N, 阻力f。建坐标如图,将重力G分解:
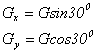

根据运动学规律: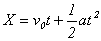 ,求得加速度为: ,求得加速度为: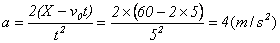 ,代入上述动力学方程(1)求得: ,代入上述动力学方程(1)求得:
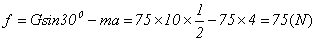
注:本题主要是运用矢量的加法和加法解决运动合力的关系问题。较多地运用正交分解法和同一直线上的矢量加减法。解决此问题,首先要受力分析;然后求合力,而求合力的是需要先将力正交分解,把一个平面矢量的合成问题转化为两条直线上的矢量加法问题,使运算更简单,这个方法在物理中经常使用 | 
