|
§3.1.1两角和与差的余弦(一)
(一)教学目标
1、知识目标
(1)利用向量的数量积去发现两角差的余弦公式
(2)灵活正反运用两角差的余弦
2、能力目标
(1)通过求两个向量的夹角,发现两角差的余弦,培养学生融会贯通的能力。
(2)培养学生注重知识的形成过程。
3、情感目标:通过公式的推导,更进一步发现“向量”的强大作用。
(二)教学重点、难点
重点: (1)两角差的余弦
(2)灵活应用两角差的公式解决问题
难点: (1)两角差的余弦的推导
(2)两角差的余弦的灵活应用
(三)教学方法
本节主要是采用数形结合的思路,由代数的精密推导和几何的直观性,推导出两角差的余弦,使学生养成数形结合的习惯;另外,整体上是由特殊到一般,再由一般回归特殊应用的辩证唯物思想的方法。这样学生易接受。
(四)教学内容安排
|
教学环节 |
教学内容 |
师生互动 |
设计意图 |
|
复习引入 |
复习向量的数量积以及它的主要作用:求两个向量夹角的余弦值。
正板书:
例1:已知向量
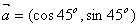 , ,
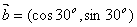 ,求< ,求< >的余弦 >的余弦
解: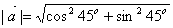 =1 =1
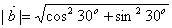 =1 =1
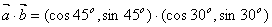 = =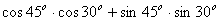
=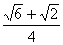
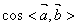 = =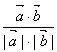 = =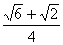
即:cos15o
=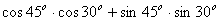
=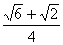 |
学生回答,老师写副板书;写出向量的数量积以及它的变形(求夹角的余弦值)
师:求向量夹角的余弦值,应具备哪些条件?
生:应该求出两个向量的数量积以及它们各自的模
师:回答很好。我们先来求这两个向量的模以及它们的数量积。
生:上黑板板书。
师:下面我们来看看这道题的几何解释。
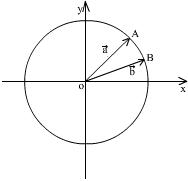
由上面的代数解法可知,它们的模都是1,这说明它们都在单位圆上。(给出幻灯片或边说边画)
如果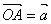 , ,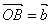 ,则∠AOB=< ,则∠AOB=< >=15o;通过图形可知,实际上我们求的 >=15o;通过图形可知,实际上我们求的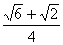 就是cos15o 就是cos15o
|
以旧带新,注意创设问题的情境,为引出新课程打基础。
通过这道题一来巩固向量积,二来为引出两角差的余弦做好准备。
先通过代数方法来求;
从几何图形上直观的反应这道题。 | |

