|
§3.1.2两角和与差的正弦
(一) 教学目标
1 . 知识目标:掌握公式的推倒过程,会用公式求值
2.能力目标:培养学生的观察、分析、类比、联想能力;间接推理能力(即不能直接套用公式,需要变化条件,寻找依据,才能推出结论)
3.情感目标:发展学生的正向、逆向思维和发散思维的能力,构建良好的数学思维品质。
(二)教学重点、难点
重点:两角和与差的正弦公式的应用和旋转变换公式
难点:利用两角和的正弦公式变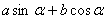 为一个角的三角函数的形式 为一个角的三角函数的形式
(三)教学方法
观察、归纳、启发、探究相结合的教学方法
(四)教学过程
|
教学
环节 |
教学内容 |
师生互动 |
设计意图 |
|
复
习
引
入 |
 复习公式 复习公式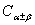 和诱导公式 和诱导公式
并由此提出问题,引入新课 |
先让学生默写两角和与差的余弦公式,然后指出这一组公式是讨论复角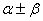 的余弦函数与单角 的余弦函数与单角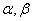 的正弦、余弦函数间的关系,且此关系对任意的 的正弦、余弦函数间的关系,且此关系对任意的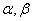 都成立,那么,在这组公式基础上能否结合同角的正弦函数和余弦函数的关系推导出复角 都成立,那么,在这组公式基础上能否结合同角的正弦函数和余弦函数的关系推导出复角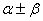 的正弦函数与单角 的正弦函数与单角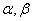 的正弦、余弦函数间的关系呢? 的正弦、余弦函数间的关系呢? |
以旧引新,注意创设问题的情景,通过设疑,引导学生开展积极的思维活动。 |
|
公
式
的
推
导
及
理
解 |
公式的推导 |
教师板书课题师生共同完成公式的证明
证明后思考讨论:
1. 证明此公式的关键步骤是什么?
2. 与 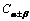 这组公式相比有何异同点? 这组公式相比有何异同点?
3. 公式有何用处?有何变形?
由学生讨论,教师点评,主要归纳如下几点
(1) 这组公式推导的关键是使用同角的正弦函数和余弦函数之间的关系达到了转换名称的目的
(2) 与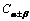 相比结构非常相似。但在函数名称的排列位置与连接符号都有所不同 相比结构非常相似。但在函数名称的排列位置与连接符号都有所不同
此公式可以用来求值,进行三角变换等,注意公式的逆向形式 |
通过对三个问题的分析、讨论使学生对公式有一个清晰完整的认识,为公式的灵活应用打下基础。 | |

