|
3.1.3两角和与差的正切
一、教学目标:
1、知识与技能:
⑴掌握公式及其推导过程,理解公式成立的条件;会用公式求值。
⑵培养学生的观察、分析、类比、联想能力;间接推理能力;自学能力。
2、过程与方法:由学生熟知的两角和与差的正弦、余弦公式,引导学生推导出两角和与差的正切公式,通过教师的提问,学生观察,分析,讨论及练习。及时搜集反馈信息,动态调整教学过程,引导学生攻克难点,掌握重点。
3、情感态度、价值观:发展学生的正向、逆向思维和发散思维能力,构建良好的数学思维品质。
二、教学重点:公式的结构特点及其推导方法、成立条件,运用公式求值。
教学难点:公式的逆向和变形应用。
三、教学过程:
1、复习引入
复习:两角和与差的正、余弦公式Sa+b ,Sa-b , Ca+b ,Ca-b
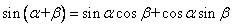
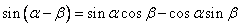
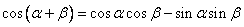
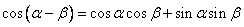
提出问题:复角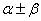 与单角 与单角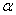 , ,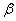 的正弦、余弦函数存在以上关系,那么能否用 的正弦、余弦函数存在以上关系,那么能否用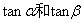 来表示 来表示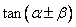 呢? 呢?
2、两角和与差正切公式的推导及理解 Ta+b ,Ta-b
⑴tan(a+b)公式的推导(让学生回答) ∵cos (a+b)¹0 |

