|
●课 题
等差数列的前n项和(二)
●教学目标
(一)教学知识点
等差数列的前n项和公式Sn= =na1+ =na1+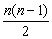 d . d .
(二)能力训练要求
1.进一步熟练掌握等差数列的通项公式和前n项和公式.
2.了解等差数列的一些性质,并会用它们解决一些相关问题.
(三)德育渗透目标
提高学生的应用意识.
●教学重点
熟练掌握等差数列的求和公式.
●教学难点
灵活应用求和公式解决问题.
●教学方法
讲练结合法
结合具体例子讲解分析问题,解决问题的方法,从而提高学生分析问题,解决问题的能力.
●教具准备
投影片两张
第一张:
[例1]求集合M={m|m=7n,n∈N*,且m<100}的元素个数,并求这些元素的和.
[例2]已知一个等差数列的前10项的和是310,前20项的和是1220,由此可以确定求其前n项和的公式吗?
第二张:
[例3]已知数列{an}是等差数列,Sn是其前n项和.
求证:S6,S12-S6,S18-S12成等差数列,设其k∈N*,Sk,S2k-Sk,S3k-S2k成等差数列吗?
●教学过程
Ⅰ.复习回顾
[师]请同学们回顾一下等差数列的通项公式及前n项和公式.
[生]通项公式:an=a1+(n-1)d,求和公式:Sn= =na1+ =na1+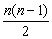 d d
Ⅱ.讲授新课 |

