|
14.3(2)空间直线和平面的位置关系
上海市南洋中学 刘小萍
一、教学内容分析
空间的角,是对由点、直线、平面所组成的空间图形中各种元素间的位置关系进行定量分析的一个重要概念,由它们的定义,可得其取值范围,前面我们已研究了两异面直线所成的角,本节研究直线与平面所成的角
课本通过一个标枪的实例说明了直线与平面所成的角有它的实际背景.接着借助图14—22引出了一系列概念.
对于空间角的计算,总是通过一定的手段将其转化为一个平面内的角,并把它置于一个平面图形,而且是一个三角形的内角来解决,而这种转化就是利用直线与平面的平行与垂直来实现的,因此求这些角的过程也是直线、平面的平行与垂直的重要应用.通过空间角的计算和应用进一步培养运算能力、逻辑推理能力及空间想象能力.
求直线和平面所成的角的方法是:
射影转化法.具体步骤如下:①找过斜线上一点与平面垂直的直线;②连结垂足和斜足,得出斜线在平面的射影,确定出所求的角;
③把该角置于三角形中计算.
注:①斜线和平面所成的角,是它和平面内任何一条直线所成的一切角中的最小角,即若θ为线面角,α为斜线与平面内任何一条直线所成的角,则有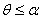 . .
二、教学目标设计
理解并掌握斜线在平面内的射影、直线和平面所成角的概念,根据概念先找直线射影后确定线面夹角从而熟练求解直线和平面所成角,培养化归能力、分析能力、观察思考能力和空间想象能力等.
培养立体感、数学美感,提高学生学习数学特别是立体几何的兴趣. 三、教学重点及 |

