|
一元二次不等式的解法
【复习目标】掌握一元二次不等式的解法;
会解决含参一元二次不等式的问题;
会解决由一元二次不等式的解求参数的值或范围的问题.
【学习重点】一元二次不等式的解法;分类讨论的思想
【学习难点】含参一元二次不等式的问题
【考试要点】
(1)一元二次函数、一元二次方程、一元二次不等式三者之间的关系:
|
一元二次方程ax2+bx+c=0(a>0)解的情况 |
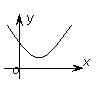 一元二次函数y=ax2+bx+c(a>0)的图象 一元二次函数y=ax2+bx+c(a>0)的图象
|
一元二次不等式ax2+bx+c>0(a>0)解集情况 |
一元二次不等式ax2+bx+c<0(a>0)解集情况 |
|
ax2+bx+c=0没有实数根 |
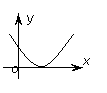
|
|
|
|
ax2+bx+c=0有二等实根 |
|
|
|
|
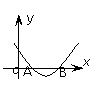
ax2+bx+c=0有二不等实根(x12) |
|
|
|
(2)解一元二次不等式的步骤:先判断二次项系数的正负;再看判别式;最后比较根的大小.解集要么为两根之外,要么为两根之内.具体地:
①设不等式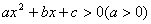 ,对应方程 ,对应方程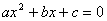 有两个不等实根 有两个不等实根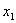 和 和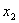 ,且 ,且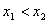 ,则不等式的解为: ,则不等式的解为: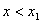 或 或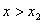 (两根之外) (两根之外)
②设不等式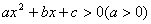 ,对应方程 ,对应方程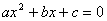 有两个不等实根 有两个不等实根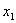 和 和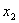 ,且 ,且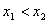 ,则不等式的解为: ,则不等式的解为: 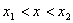 (两根之内) (两根之内) 说明:①若不等式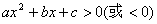 中,a 中,a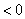 ,可在不等式两边乘 ,可在不等式两边乘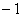 转化为二次项系 转化为二次项系 |

