|
v
集合五问
集合是现代数学中一个原始的、不加定义的概念。教材上给出“集合”的概念,只是对集合描述性的说明。初次接触集合感到比较抽象,难以把握。实质上,集合元素的三个性质是我们解决集合有关概念问题的重要依据。子集、真子集的定义是解决两个集合之间关系的法宝。下面通过五个问题对同学们容易忽略的知识进行解答,以期对同学们有所帮助。
一问:你已掌握集合概念中所描述的集合的全体性了吗?
例1:函数y=x2+x-1的定义域为( )。
①{R} ②{一切实数} ③ R ④{实数} ⑤ 实数
A ①② B ②③
C ③④ D ④⑤
分析:任何一个实数都能使函数y=x2+x-1有意义,故函数的定义域应为全体实数。所以③正确。R与一切实数都表示一个整体,它们是一个集合,放在大括号内是表示以集合为元素的单元素集,所以①②不正确。④表示实数的全体,正确。⑤表示元素,不正确。
答案:C
点评:用符号{}表示集合时,它表示大括号内元素的全体。在表示定义域时,大括号内的元素应是使函数有意义的实数,而不应该是一个集合。
二问:用描述法表示集合时,你注意到代表元素的代表性了吗?
例2:设集合A={x│y=x2-1},B={y│y=x2-1},C={(x,y)│y=x2-1},D={y=x2-1}
分别写出集合A、B、C、D的意义,A表示 ,B表示 ,C表示 ,D表示 。
分析:集合表示的是代表元素的全体,竖线后面表示代表元素满足的条件,故A表示自变量x的全体是函数的定义域,B表示因变量y的全体是函数的值域,C表示满足函数的点的全体是函数的图像,D是用列举法表示以方程y=x2-1为元素的单元素集。
答案:A表示函数的定义域,
B表示函数的值域,
C表示函数的图像,
D表示以方程y=x2-1为元素的单元素集。
点评:集合的代表元素规定了集合的类型。
三问:你注意到集合元素的互异性了吗?
例3:设集合A={1,3,a},B={1,a2-a+1},若B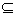 A,求a的值。 A,求a的值。
分析:因为B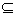 A,所以B中的元素1,a2-a+1都是A中的元素,但是要考虑到元素的互异性。 A,所以B中的元素1,a2-a+1都是A中的元素,但是要考虑到元素的互异性。 |

