|
v
反函数性质的应用
只有定义域和值域一一对应的函数才有反函数,反函数是由原函数派生出来的,它的定义域、对应法则、值域完全由原函数决定。因此利用这一关系可以将原函数的问题与反函数的问题相互转化,使问题容易解决。现在看一下反函数性质的应用。
⒈利用反函数的定义求函数的值域
例1:求函数y=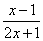 的值域。 的值域。
分析:这种函数可以利用分离常数法或反函数法求值域,下面利用反函数法来求解。解:由y=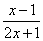 得y(2x+1)=x-1 得y(2x+1)=x-1
∴(2y-1)x=-y-1
∴x=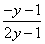
∵x是自变量,是存在的,
∴2y-1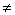 0,∴ y 0,∴ y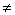 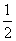 。 。
故函数y=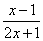 的值域为:{y│y 的值域为:{y│y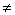 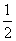 }。 }。
点评:形如y=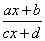 的函数都可以用反函数法求它的值域。 的函数都可以用反函数法求它的值域。
⒉原函数与反函数定义域、值域互换的应用
例2:已知f(x)=4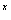 -2 -2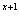 ,求f ,求f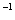 (0)。 (0)。
分析:要求f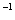 (0),只需求f(x)=0时自变量x的值。 (0),只需求f(x)=0时自变量x的值。
解:令f(x)=0,得4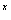 -2 -2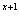 =0,∴2 =0,∴2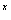 (2 (2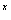 -2)=0, -2)=0,
∴2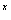 =2或2 =2或2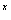 =0(舍), =0(舍),
∴x=1。
故f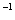 (0)=1。 (0)=1。 |

