|
函数的基本性质(一)
基础知识:
函数的性质通常是指函数的定义域、值域、解析式、单调性、奇偶性、周期性、对称性等等,在解决与函数有关的(如方程、不等式等)问题时,巧妙利用函数及其图象的相关性质,可以使得问题得到简化,从而达到解决问题的目的.
关于函数的有关性质,这里不再赘述,请大家参阅高中数学教材及竞赛教材:陕西师范大学出版社 刘诗雄《高中数学竞赛辅导》、刘诗雄、罗增儒《高中数学竞赛解题指导》.
例题:
1. 已知f(x)=8+2x-x2,如果g(x)=f(2-x2),那么g(x)( )
A.在区间(-2,0)上单调递增 B.在(0,2)上单调递增
C.在(-1,0)上单调递增 D.在(0,1)上单调递增
提示:可用图像,但是用特殊值较好一些.选C
2. 设f(x)是R上的奇函数,且f(x+3)=-f(x),当0≤x≤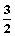 时,f(x)=x,则f(2003)=( ) 时,f(x)=x,则f(2003)=( )
A.-1 B.0 C.1 D.2003
解:f(x+6)=f(x+3+3)=-f(x+3)=f(x)
∴ f(x)的周期为6
f(2003)=f(6×335-1)=f(-1)=-f⑴=-1
选A
3. 定义在实数集上的函数f(x),对一切实数x都有f(x+1)=f(2-x)成立,若f(x)=0仅有101个不同的实数根,那么所有实数根的和为( )
A.150 B.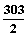 C.152 D. C.152 D.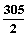
提示:由已知,函数f(x)的图象有对称轴x=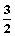
于是这101个根的分布也关于该对称轴对称.
即有一个根就是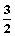 ,其余100个根可分为50对,每一对的两根关于x= ,其余100个根可分为50对,每一对的两根关于x=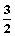 对称 对称
利用中点坐标公式,这100个根的和等于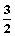 ×100=150 ×100=150
所有101个根的和为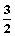 ×101= ×101=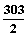 .选B .选B 实数x,y满足x2=2xsin(xy)-1,则x1998+6sin5y=______________.
解:如果x、y不是某些特殊值,则本题无法(快速)求解
注意到其形式类似于 |

