|
5.2(1) 任意角的三角比
上海市杨浦高级中学 方耀华
一、教学内容分析
通过平面直角坐标系定义了任意角的正弦、余弦、正切、余切、正割、余割六个三角比,并利用与单位圆有关的线段,将前三个三角比的值分别用它们的几何形式表示出来;接着着重研究正弦、余弦、正切这三个三角比的条件和其在各个象限的符号;并根据三角比的定义,得出“终边重合的角的同一三角比的值相等”的结论及把此结论表示成为第一组诱导公式(公式一).
二、教学目标设计
(1) 掌握任意角的正弦、余弦、正切的定义,了解如何利用与单位圆有关的有向线段,将任意角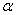 的正弦、余弦、正切值分别用正弦线、余弦线、正切线表示出来; 的正弦、余弦、正切值分别用正弦线、余弦线、正切线表示出来;
(2) 了解余切、正割、余割的定义;掌握正弦、余弦、正切等三角比对角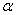 的条件要求; 的条件要求;
(3) 体会同一角三角比的值,不因在其终边上取点的变化而变化,从而启示在研究问题时,要能在千变万化中,抓住事物的本质属性,不被表面现象所迷惑.
三、教学重点及难点
重点:任意角的三角比的定义.
难点:用单位圆中的有向线段表示角的正弦、余弦、正切值.
四、教学流程设计
|

