|
v
6.4反三角函数(2)——反余弦函数、反正切函数
 上海市交通大学附属中学 曹建华 上海市交通大学附属中学 曹建华
一、教学内容分析
根据反函数的概念,余弦函数y=cosx(x∈R)没有反函数.但是如果我们适当选取实数集R的一个子集[0,π],那么函数y=cosx,x∈[0,π]就存在反函数,为什么要选取[0,π],教师要引导学生作必要的讨论和说明.类比反正弦函数的定义,我们把函数y=cosx,x∈[0,π]的反函数叫做反余弦函数,记作y=arccosx,x∈[-1,1],学生对符号的arccosx的理解比较困难,前面符号中的x必须满足|x|≤1,arccosx是[0,π]上的一个角的弧度数,这个角的余弦值为x.根据互为反函数间的图像关系,函数y=arccosx, x∈[-1,1]的图像和函数y =cosx,x∈[0,π]的图像应该关于直线y=x对称,这样容易作出反余弦函数的图像,根据其图像可以得到反余弦函数y=arccosx,x∈[-1,1]既不是奇函数也不是偶函数,但是单调递减.类似地,把正切函数y=tanx,x∈(- x∈[-1,1]的图像和函数y =cosx,x∈[0,π]的图像应该关于直线y=x对称,这样容易作出反余弦函数的图像,根据其图像可以得到反余弦函数y=arccosx,x∈[-1,1]既不是奇函数也不是偶函数,但是单调递减.类似地,把正切函数y=tanx,x∈(-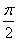 , ,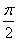 )的反函数叫做反正切函数,记作y=arctanx,x∈(-∞,∞),根据互为反函数间的图像关系,函数y=arctanx,x∈(-∞,∞)的图像和函数y = tanx,x∈(- )的反函数叫做反正切函数,记作y=arctanx,x∈(-∞,∞),根据互为反函数间的图像关系,函数y=arctanx,x∈(-∞,∞)的图像和函数y = tanx,x∈(-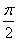 , ,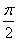 )的图像应该关于直线y=x对称,这样容易作出反正切函数的图像,根据其图像可以得到反正切函数y= arctanx,x∈(-∞,∞)是奇函数,单调递增. )的图像应该关于直线y=x对称,这样容易作出反正切函数的图像,根据其图像可以得到反正切函数y= arctanx,x∈(-∞,∞)是奇函数,单调递增.
二、教学目标设计
1.理解函数y=cosx(x∈R),y=tanx(x≠kπ+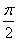 ,k∈Z)没有反函数;理解函数y=cosx, x∈[0,π],y=tanx,x∈(- ,k∈Z)没有反函数;理解函数y=cosx, x∈[0,π],y=tanx,x∈(-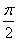 , ,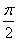 )有反函数;理解反余弦函数y=arccosx,反正切函数y=arctanx的概念,掌握反余弦函数的定义域是[-1,1],值域是[0,π];反正切函数的定义域是(-∞,∞),值域是(- )有反函数;理解反余弦函数y=arccosx,反正切函数y=arctanx的概念,掌握反余弦函数的定义域是[-1,1],值域是[0,π];反正切函数的定义域是(-∞,∞),值域是(-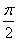 , ,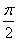 ). ).
2.知道反余弦函数y=arccosx ,x∈[-1,1]和反正切函数y= arctanx,x∈(-∞,∞)的图像.
3.掌握等式cos(arccosx)=x,x∈[-1,1],arccos(-x)=π-arccosx,x∈[-1,1]和tan(arctanx)=x,x∈(-∞,∞),arctan(-x)=- arctanx,x∈(-∞,∞).
4.能够熟练计算特殊值的反余弦函数值和反正切函数值,并能用反余弦函数值和反正切函数值表示角. 5. |

