|
西安交大阳光中学2009——2010 学年度第二学期
数学导学案设计
年级:高一 科目:数学
|
第三章第节 |
课题名称 |
简单线性规划的应用 |
|
授课时间 |
第 周星期 第 节 |
课型 |
新授课 |
主备课人 |
卫娟莲 |
|
学习目标 |
从实际情境中抽象出简单线性规划问题并解决 |
|
重点难点 |
列出约束条件及写出目标函数 |
|
学习过程
与方法 |
1. 自主学习:
若实数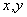 满足 满足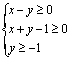 求 求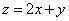 的最大值及最小值 的最大值及最小值
|
|
2.精讲互动:
例1:某工厂生产甲、乙两种产品.已知生产甲种产品1t需消耗A种矿石10t、B种矿石5t、煤4t;生产乙种产品1吨需消耗A种矿石4t、B种矿石4t、煤9t.每1t甲种产品的利润是600元,每1t乙种产品的利润是1000元.工厂在生产这两种产品的计划中要求消耗A种矿石不超过300t、消耗B种矿石不超过200t、消耗煤不超过360t.甲、乙两种产品应各生产多少(精确到0.1t),能使利润总额达到最大?
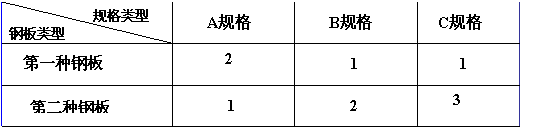
例2 要将两种大小不同规格的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示 :
在可行域内找出最优解、线性规划整数解问题的一般方法是:
1.若区域“顶点”处恰好为整点,那么它就是最优解;(在包括边界的情况下)
2.若区域“顶点”不是整点或不包括边界时,应先求出该点坐标,并计算目标函数值Z,然后在可行域内适当放缩目标函数值,使它为整数,且与Z最接近,在这条对应的直线中,取可行域内整点,如果没有整点,继续放缩,直至取到整点为止。
3.在可行域内找整数解,一般采用平移找解法,即打网络、找整点、平移直线、找出整数最优解
| |

