|
学习过程
与方法 |
自主学习:
1) a>b,b>c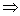 a c (2)a>b a c (2)a>b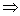 a+c b+c; a+c b+c;
(3)a>b,c>0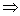 ac bc; (4)a>b,c<0 ac bc; (4)a>b,c<0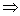 ac bc. ac bc.
推论:(1) a>c,c>d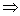 a+c b+d; (2) a>b>0,c>d>0 a+c b+d; (2) a>b>0,c>d>0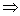 ac bd; ac bd;
(3)a>b>0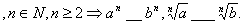
经常用“不等式取倒数”的性质: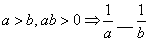
一元二次不等式的解法
1.一元二次不等式(a>0)的解集如下表:
2.一元二次不等式恒成立的条件:
(1)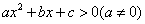 恒成立的充要条件是 ; 恒成立的充要条件是 ;
(2)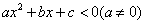 恒成立的充要条件是 . 恒成立的充要条件是 .
线性规划
1.二元一次不等式(组)表示的平面区域的判别方法:
对于直线Ax+By+c=0同一侧所有点,把它的坐标(x,y)代入Ax+By+c所得值符号都相同,因此只需在直线Ax+By+c=0的某一侧取一个特殊点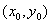 作为测试点,由 作为测试点,由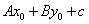 的符号就可以断定不等式解集表示的是直线哪一侧的平面区域.当 的符号就可以断定不等式解集表示的是直线哪一侧的平面区域.当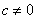 时,通常取原点(0,0)作为测试点. 时,通常取原点(0,0)作为测试点.
2.简单线性规划
(1)由二元一次不等式组成的一组约束条件称为 .要求最值的函数z=ax+by+c称为 ,由于z=ax+by+c是关于x、y的一次解析式,所以又称为 .在线性约束条件下求线性目标函数的最大值或最小值问题,统称为 .满足线性约束条件的解(x,y)叫做 .由所有可行解组成的集合叫做 ,其中,使目标函数取得最大值或最小值的可行解叫做这个问题的
|

