|
典型例题
【例1】为了了解中学生身体发育情况,对某中学60名同龄女学生作了下面的统计活动.
(1)调查者事先做好问卷;
|
 请你在下面的横线上填上自己的身高. 请你在下面的横线上填上自己的身高.
___________cm |
(2)给每个调查者发放 问卷,并进行回收; 问卷,并进行回收;
(3)对所有调查数据进行汇总.
表1-3
为了了解中学生的身体发育情况,对某中学同年龄的60名女学生的身高进行了测量,结果如下(单位:cm):
167 154 159 166 169 159 156 166 162 158
159 156 166 160 164 160 157 156 157 161
158 158 153 158 164 158 163 158 153 157
162 162 159 154 165 166 157 151 146 151
158 160 165 158 163 163 162 161 154 165
162 162 159 157 159 149 164 168 159 153
根据我们的调查目的对数据进行分析.下面我们讨论几个问题.
(1)计算她们的平均身高;
(2)计算最大值与最小值的差;
(3)统计这60名女学生的身高数据在各个小范围内所占比的大小;
(4)研究这60名女学生的身高离散程度.
解:(1)容易发现,学生身高都在160 cm左右,于是将上面各数据同时减去160,转而计算一组数值较小的新数据的平均数.
将上面各数据同时减去160,得到的一组新数据是
7 -6 -1 6 9 -1 -4 6 2 -2
-1 -4 6 0 4 0 -3 -4 -3 1
-2 -2 -7 -2 4 -2 3 -2 -7 -3
2 2 -1 -6 5 6 -3 -9 -14 -9
-2 0 5 -2 3 3 2 1 -6 5
2 2 -1 -3 -1 -1 1 4 8 -1 -7
计算这组新数据的平均数得
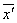 = =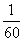 [7+(-6)+(-1)+…+(-7)]= [7+(-6)+(-1)+…+(-7)]=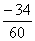 ≈-0.6. ≈-0.6.
于是求得平均数应该是
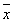 = =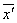 +160≈159(cm). +160≈159(cm).
(2)上面身高最大值为169 cm,最小值为146 cm,它们的差为169-146=23(cm).
(3)为了统计这60名女学生的身高数据在各个小范围内所占比的大小,先要决定组距与组数.根据情况选 取组据为3 cm,把她们的身高分为8组,所分的8个小组 取组据为3 cm,把她们的身高分为8组,所分的8个小组 是: 是:
145.5~148.5 148.5~151.5 151.5~154.5
154.5~157.5 157.5~160.5 160.5~163.5
163.5~166.5 166.5~169.5
表1-4 频率分布表
|
分 组 |
频数累计 |
频 数 |
频 率 |
|
145.5~148.5 |
一 |
1 |
0.017 |
|
148.5~151.5 |
正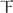
|
3
|
0.050
|
|
151.5~154.5 |
正一 |
6 |
0.100 |
|
154.5~157.5 |
正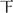 |
 8 8
|
0.133 |
|
157.5~160.5 |
正正正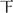 |
18 |
0.300 |
|
160.5~163.5 |
正正一 |
11 |
0.183 |
|
163.5~166.5 |
正正 |
10 |
0.167 |
|
166.5~169.5 |
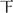
|
3 |
0.050 |
下面给出几种统计图来表示各个小范围内所占比的大小,你认为哪一个好一些?
[来源:学科网ZXXK]
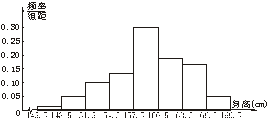
图1-1-2

图1-1-3
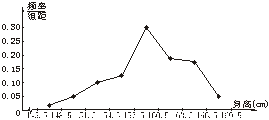
图1-1-4
(4)为了研究身边60名女学生身高的离散程度,需要求这组数据的方差.
S2=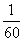 [(167-159)2+(154-159)2+…+(153-159)2]≈24.2. [(167-159)2+(154-159)2+…+(153-159)2]≈24.2.
方差比较大,说明数据波动较大,也就是说各个学生的身高发展情况不均衡.
【例2】为了了解中学生的心理发展状况,对某中学60名中学生作了下面的统计活动.
(1)调查者事先做好问卷;
|
请把与你现在心理压力状况相符的选项选出 来打上“√”. 来打上“√”.
1.心理很轻松 2.心理较轻松
3.有些压 力 力  4.有较大的压力 4.有较大的压力
5.压力很大,心情烦燥 |
(2)给每个调查者发放问卷,并进行回收;
(3)对所有调查数据进行汇总.
|
选项 |
1 |
2 |
3 |
4 |
5 |
|
统计结果 |
|
正 |
正正正正 |
正正正 |
正正 |
|
人数 |
4 |
5 |
24 |
17 |
10[来源:学科网] |
统计问题:
(1)计算出选择各个选项的百分比(用四舍五入方法保留到百分数的整数位);
 (2)用下面的统计图表示上面的数据时,你觉得哪种统计图更适合?并说明理由; (2)用下面的统计图表示上面的数据时,你觉得哪种统计图更适合?并说明理由;
(3)请你分析这批数据的集中趋势与离散程度;
(4)从上面的数据能否看出,选哪些选项的人数多些?你能得出什么结论?
解:(1)计算出选各个选项的百分比.
|
选项 |
1 |
2 |
3 |
4 |
5 |
|
人数/人 |
4 |
5 |
24 |
17 |
10 |
|
百分比% |
7 |
8 |
40 |
28 |
17 |
(2)统计图如下,由于这个问题所关心的是选择各个数的人占总数的百分比情况,因此选择扇形统计图比较合适,它能够比较清楚地表达百分比的情况.
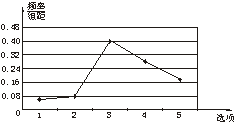
图1-1-5
(3)平均数为
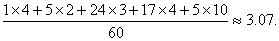
方差为S2=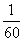 [(1-3.07)2+(1-3.07)2+…+(5-3.07)2]≈1.249. [(1-3.07)2+(1-3.07)2+…+(5-3.07)2]≈1.249.
(4)从扇形统计图上可以看出,选择“有些压力”和“有较大压力”的人数较多,选择“心理很轻松”“心理较轻松”的人数较少,值得注意的是选择“压力很大,心情烦燥”的也不少,说明绝大多数同学在学习中有压力,不少同学的心理压力值得我们关注.从平均数和方差中也能看出这些问题.
建议教育部门对中学生的心理状况加以关注,切实减轻各方面的负担,包括教育收费问题、课业负担等,让学生在轻松、健康的心情下自我发展.
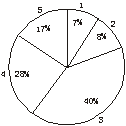
图1-1-6
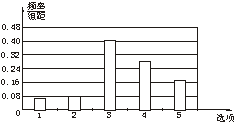
图1-1-7 |
规律发现
可对某中学16岁女生发60份问卷进行调查.
注意发放问卷的“随机”性,并全部收回.
平均数反映数据的集中趋势,最大值与最小值的差反映数据的 范围,用统计图反映各个小范围内百分比,方差反映数据波动大小. 范围,用统计图反映各个小范围内百分比,方差反映数据波动大小.
[来源:学科网ZXXK]
这种计算平均数的方法是常用的数学计算方法,科学简便.
[来源:Zxxk.Com]
将一批数据分组,一般数据越多,分组也越多.当数据在100个以内时,常分成5~12组.
频率也就是该组数据所占总数的百分比.
各个小长方形的面积等于相应各组的频率.这样,频率直方图就以图形面积形式反映了数据落在各个小组内的频率的大小.
说明受遗传因素影响和后天营养状况影响,学生的身高有较大的差别.
根据不同的目的,可以设计不同的问卷,学生的心理状况是大家比较关心的问题,应该加以关注.
我们通过计算各选项的百分比、平均数、方差,用数据来反映当今学生的心理状况,得出我们关心的信息,研究当今中学生的心理状况,找出解决问题的方法.

我们可以根据我们关心的社会政治、经济、学习、生活等问题进行问卷调查,并统计得出可靠信息,帮助我们找出解决问题的方法.
同学们,你的心理负担是否也过重呢?
| 
