西安交大阳光中学高一年级数学导学案
课题:从力做的功到向量的数量积 时间:
一、学习目标: 理解平面向量数量积的概念及其几何意义掌握数量积的运算法则了解平面向量的数量积与投影的关系
二、重难点 向量数量积的含义及其物理意义、几何意义;运算律
三、知识链接
四、学习过程
1.已知两个非零向量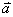 与 与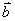 ,它们的夹角为 ,它们的夹角为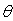 ,则把数量_____________叫做向量 ,则把数量_____________叫做向量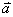 与 与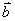 的数量积(或内积). 的数量积(或内积).
规定:零向量与任一向量的数量积为_____.
2.已知两个非零向量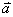 与 与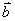 ,作 ,作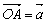 , ,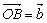 ,则________________________叫做向量 ,则________________________叫做向量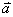 与 与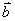 的夹角. 的夹角.
当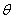 =0°时 =0°时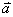 与 与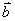 _____,当 _____,当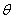 =180°时 =180°时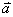 与 与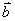 ____;当 ____;当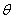 =90°时则称向量 =90°时则称向量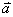 与 与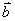 ____. ____.
3.对于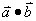 = =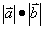 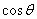 ,其中______叫做 ,其中______叫做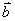 在 在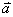 方向上的投影. 方向上的投影.
4.平面向量数量积的性质
若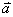 与 与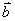 是非零向量, 是非零向量,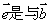 方向相同的单位向量, 方向相同的单位向量,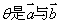 的夹角,则: 的夹角,则:
①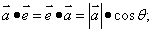 ② ②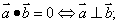 ③ ③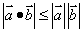
④若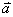 与 与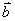 同向,则 同向,则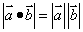 ;若 ;若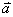 与 与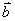 反向,则 反向,则 ; ;
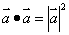 或 或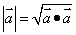 ⑤设 ⑤设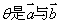 的夹角,则 的夹角,则
5.数量积的运算律
①交换律:_____________________________ ②数乘结合律:_________________________
③分配律:_____________________________ 例1:已知向量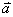 与向量 与向量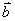 的 的 |

