|
1-5.3正弦函数的性质
一、 教学思路
【创设情境,揭示课题】
 同学们,我们在数学一中已经学过函数,并掌握了讨论一个函数性质的几个角度,你还记得有哪些吗?在上一次课中,我们已经学习了正弦函数的y=sinx在R上图像,下面请同学们根据图像一起讨论一下它具有哪些性质? 同学们,我们在数学一中已经学过函数,并掌握了讨论一个函数性质的几个角度,你还记得有哪些吗?在上一次课中,我们已经学习了正弦函数的y=sinx在R上图像,下面请同学们根据图像一起讨论一下它具有哪些性质?
【探究新知】
让学生一边看投影,一边仔细观察正弦曲线的图像,并思考以下几个问题:
(1) 正弦函数的定义域是什么?
(2) 正弦函数的值域是什么?
(3) 它的最值情况如何?
(4) 它的正负值区间如何分?
(5) ƒ(x)=0的解集是多少?
师生一起归纳得出:
1. 定义域:y=sinx的定义域为R
2. 值域:引导回忆单位圆中的正弦函数线,结论:|sinx|≤1(有界性)
再看正弦函数线(图象)验证上述结论,所以y=sinx的值域为[-1,1]
3.最值:1°对于y=sinx 当且仅当x=2kp+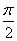 ,kÎZ时 ymax=1 ,kÎZ时 ymax=1
当且仅当时x=2kp-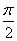 , kÎZ时 ymin=-1 , kÎZ时 ymin=-1
2°当2kp<x<(2k+1)p (kÎZ)时 y=sinx>0
当(2k-1)p<x<2kp (kÎZ)时 y=sinx<0
4.周期性:(观察图象) 1°正弦函数的图象是有规律不断重复出现的;
2°规律是:每隔2p重复出现一次(或者说每隔2kp,kÎZ重复出现)
3°这个规律由诱导公式sin(2kp+x)=sinx也可以说明
结论:y=sinx的最小正周期为2p
5.奇偶性
 sin(-x)=-sinx (x∈R) y=sinx (x∈R)是奇函数 sin(-x)=-sinx (x∈R) y=sinx (x∈R)是奇函数
6.单调性
|

