|
高三数学第二轮专题复习系列(9)—立体几何
一、考纲要求
1.掌握平面的基本性质,空间两条直线、直线和平面、两个平面的位置关系(特别是平行和垂直关系)以及它们所成的角与距离的概念.
2.对于异面直线的距离,只要求会计算已给出公垂线时的距离.
3.能运用上述概念以及有关两条直线、直线和平面、两个平面的平行和垂直关系的性质与判定,进行论证和解决有关问题.
4.会用斜二侧的画法画水平放置的平面图形(特别是正三角形、正四边形、正五边形、两个平面、直线和平面的各种位置关系的图形,能够根据图形想象它们的位置关系.
5.理解用反证法证明命题的思路,会用反证法证明一些简单的问题.
二、知识结构
1.空间多边形不在同一平面内的若干线段首尾相接所成的图形叫做空间折线.
若空间折线的最后一条线段的尾端与最初一条线段的首端重合,则叫做封闭的空间折线.
若封闭的空间折线各线段彼此不相交,则叫做这空间多边形平面,平面是一个不定义的概念,几何里的平面是无限伸展的.
平面通常用一个平行四边形来表示.
平面常用希腊字母α、β、γ…或拉丁字母M、N、P来表示,也可用表示平行四边形的两个相对顶点字母表示,如平面AC.
在立体几何中,大写字母A,B,C,…表示点,小写字母,a,b,c,…l,m,n,…表示直线,且把直线和平面看成点的集合,因而能借用集合论中的符号表示它们之间的关系,例如:
A∈l—点A在直线l上;
A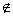 α—点A不在平面α内; α—点A不在平面α内;
l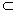 α—直线l在平面α内; α—直线l在平面α内;
a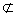 α—直线a不在平面α内; α—直线a不在平面α内;
l∩m=A—直线l与直线m相交于A点;
α∩l=A—平面α与直线l交于A点;
α∩β=l—平面α与平面β相交于直线l.
2.平面的基本性质
公理1 如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.
公理2 如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线.
公理3 经过不在同一直线上的三个点,有且只有一个平面.
根据上面的公理,可得以下推论. 推论1 |

