|
2011年高考第二轮专题复习(教学案):导数
考纲指要:
导数是高中数学中重要的内容,是解决实际问题的强有力的数学工具,运用导数的有关知识,研究函数的性质:单调性、极值和最值是高考的热 点问题。 点问题。
考点扫描:
导数在研究函数中的应用
① 结合实例,借助几何直观探索并了解函数的单调性与导数的关系;能利用导数研究函数的单调性,会求不超过三次的多项式函数的单调区间;[来源:Z.xx.k.Com]
② 结合函数的图像,了解函数在某点取得极值的必要条件和充分条件;会用导数求不超过三次的多项式函数的极大值、极小值,以及闭区间上不超过三次的多项式函数最大值、最小值;体会导数方法在研究函数性质中的一般性和有效性。
考题先知:
例1.设函数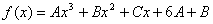 ,其中实数A、B、C满足: ,其中实数A、B、C满足:
①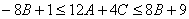 ; ② ; ②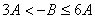 。 。
(1)求证: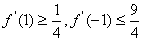 ; (2)设 ; (2)设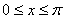 ,求证: ,求证: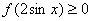 。 。
证明:(1)由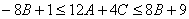 得: 得: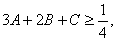 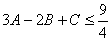 , ,
又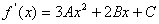 ,所以 ,所以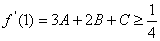 , ,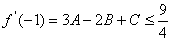 [来源:学.科.网Z.X.X.K] [来源:学.科.网Z.X.X.K]
(2)当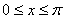 时, 时,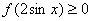 等价于当 等价于当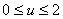 时, 时,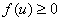 ,所以只须证明当 ,所以只须证明当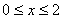 时, 时,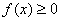 ,由②知: ,由②知: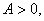 且 且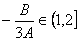 ,所以 ,所以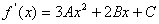 为开口向上的抛 为开口向上的抛 物线,其对称轴方程 物线,其对称轴方程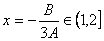 ,又由 ,又由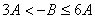 得: 得:
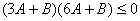 ,即 ,即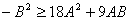  ,所以,当 ,所以,当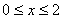 时,有 时,有
|

