|
2011年高考第二轮专题复习(教学案):解析几何
第1课时 直线与圆
考纲指要:
直线方程考察的重点是直线方程的特征值(主要是直线的斜率、截距)有关问题,以及直线间的平行和垂直的条件、与距离有关的问题。
圆的方程,从轨迹角度讲,尤其是参数问题,在对参数的讨论中确定圆的方程。能借助数形结合的思想处理直线与圆的位置关系,特别是弦长问题。
考点扫描:
1.直线方程:(1)倾斜角;(2) 斜率;(3)直线方程的五种形式。
2.圆的方程:(1)圆的标准方程;(2)圆的一般方程。
3.两点间的距离公式、点到直线的距离公式,会求两条平行直线间的距离。
4. 根据给定直线、圆的方程,判断直线与圆、圆与圆的位置关系。
考题先知:
例1.某校一年级为配合素质教育,利用一间教室作为学生绘画成果展览室,为节约经费,他们利用课桌作为展台,将装画的镜框放置桌上,斜靠展出,已知镜框对桌面的倾斜角为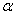 (90°≤ (90°≤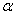 <180°)镜框中,画的上、下边缘与镜框下边缘分别相距a m,b m,(a>b) 问学生距离镜框下缘多远看画的效果最佳? <180°)镜框中,画的上、下边缘与镜框下边缘分别相距a m,b m,(a>b) 问学生距离镜框下缘多远看画的效果最佳?
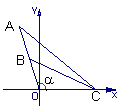 分析 欲使看画的效果最佳,应使∠ACB取最大值,欲求角的最值,又需求角的一个三角函数值 分析 欲使看画的效果最佳,应使∠ACB取最大值,欲求角的最值,又需求角的一个三角函数值
解 建立如图所示的直角坐标系,AO为镜框边,AB为画的宽度,O为下边缘上的一点,在x轴的正半轴上找一点C(x,0)(x>0),欲使看画的效果最佳,应使∠ACB取得最大值
由三角函数的定义知 A、B两点坐标分别为(acos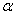 ,asin ,asin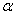 )、 )、
(bcos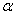 ,bsin ,bsin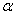 ),于是直线AC、BC的斜率分别为 ),于是直线AC、BC的斜率分别为
kAC=tanXCA=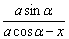 , ,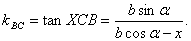
于是
tanACB=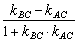 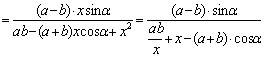 由 |

