|
2011年高考第二轮专题复习(教学案):平面向量
考纲指要:
重点考察向量的概念、向量的几何表示、向量的加减法、实数与向量的积、两个向量共线的充要条件、向量的坐标运算等。
考点扫描:
1.向量的概念:①向量;②零向量;③单位向量;④平行向量(共线向量);⑤相等向量。
2.向量的运算:(1)向量加法;(2)向量的减法;(3)实数与向量的积。
3.基本定理:(1)两个向量共线定理;(2)平面向量的基本定理。
4.平面向量的坐标表示。
5.向量的数量积:(1)两个非零向量的夹角;(2)数量积的概念;(3)数量积的几何意义;(4)向量数量积的性质;(5)两个向量的数量积的坐标运算;(6)垂直:如果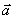 与 与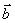 的夹角为900则称 的夹角为900则称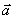 与 与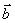 垂直,记作 垂直,记作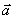 ⊥ ⊥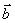 。 。
6.向量的应用:(1)向量在几何中的应用;(2)向量在物理中的应用。
考题先知:
例1. 已知二次函数f(x)=x2-2x+6,设向量a=(sinx,2),b=(2sinx,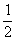 ),[来源:Zxxk.Com] ),[来源:Zxxk.Com]
c=(cos2x,1) ,d=(1,2).当x∈[0,π]时,不等式f(a·b)>f(c·d ,d=(1,2).当x∈[0,π]时,不等式f(a·b)>f(c·d )的解集为___________.[来源:学科网] )的解集为___________.[来源:学科网]
解:a·b=2sin2x+1≥1, c·d=cos2x+1≥1 ,f(x)图象关于x=1对称,
∴f(x)在(1,+∞)内单调递增.
由f(a·b)>f(c·d)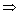 a·b>c·d,即2sin2x+1>2cos2x+1, a·b>c·d,即2sin2x+1>2cos2x+1,
又∵x∈[0, π] ,∴x∈( π] ,∴x∈(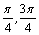 ).故不等式的解集为( ).故不等式的解集为(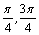 ). ).
例2.求函数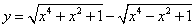 的值域. 的值域. 分析:由于向 量沟通了代数与几何的内在联系,因此本题利用向量的有关知识求函数的值域。[来 量沟通了代数与几何的内在联系,因此本题利用向量的有关知识求函数的值域。[来 |

