|
2011年中考数学一轮复习之函数与一元二次方程
知识考点:
1、理解二次函数与一元二次方程之间的关系;
2、会结合方程根的性质、一元二次方程根的判别式,判定抛物线与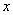 轴的交点情况; 轴的交点情况;
3、会利用韦达定理解决有关二次函数的问题。
精典例题:
【例1】已抛物线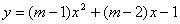 ( ( 为实数)。 为实数)。
(1) 为何值时,抛物线与 为何值时,抛物线与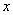 轴有两个交点? 轴有两个交点?
(2)如果抛物线与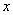 轴相交于A、B两点,与 轴相交于A、B两点,与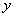 轴交于点C,且△ABC的面积为2,求该抛物线的解析式。 轴交于点C,且△ABC的面积为2,求该抛物线的解析式。
分析:抛物线与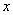 轴有两个交点,则对应的一元二次方程有两个不相等的实数根,将问题转化为求一元二次方程有两个不相等的实数根 轴有两个交点,则对应的一元二次方程有两个不相等的实数根,将问题转化为求一元二次方程有两个不相等的实数根 应满足的条件。 应满足的条件。
略解:(1)由已知有 ,解得 ,解得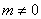 且 且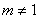
(2)由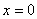 得C(0,-1) 得C(0,-1)
又∵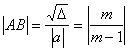
∴
∴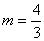 或 或
∴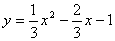 或 或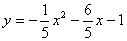
【例2】已知抛物线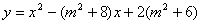 。 。
(1)求证:不论 为任何实数,抛物线与 为任何实数,抛物线与 轴有两个不同的交点,且这两个点都在 轴有两个不同的交点,且这两个点都在 轴的正半轴上; 轴的正半轴上;
(2)设抛物线与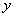 轴交于点A,与 轴交于点A,与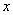 轴交于B、C两点,当△ABC的面积为48平方单位时,求 轴交于B、C两点,当△ABC的面积为48平方单位时,求 的值。 的值。
(3)在(2)的条件下,以BC为直径作⊙M,问⊙M是否经过抛物线的顶点P?
解析:(1)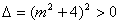 ,由 ,由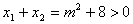 , ,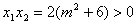 可得证。 可得证。
(2)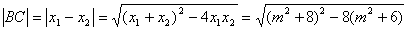
=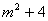
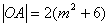
又∵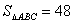
∴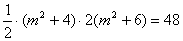
解得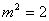 或 或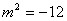 (舍去) (舍去)
∴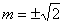
(3)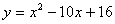 ,顶点(5,-9), ,顶点(5,-9),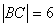
∵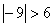
∴⊙M不经过抛物线的顶点P。
评注:二次函数与二次方程有着深刻的内在联系,因此,善于促成二次函数问题与二次方程问题的相互转化,是解相关问题的常用技巧。 |

