|
24.圆与圆(一)
知识考点:
1、掌握圆与圆的五种位置关系与两圆的半径、圆心距 之间的关系,掌握圆与圆的位置关系的三种判定方法。 之间的关系,掌握圆与圆的位置关系的三种判定方法。
2、掌握相交两圆的连心线垂直平分两圆的公共弦,相切两圆的连心线必过切点等性质。
精典例题:
【例1】 已知⊙O1与⊙O2的半径长分别为方程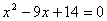 的两根,若圆心距O1O2的长为5,则⊙O1与⊙O2的位置关系如何? 的两根,若圆心距O1O2的长为5,则⊙O1与⊙O2的位置关系如何?
分析:由方程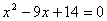 可解得 可解得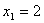 , ,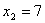 ,故 ,故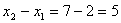 与圆心距相等,则两圆内切。 与圆心距相等,则两圆内切。
解:设⊙O1、⊙O2的半径分别为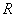 、 、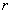 ( (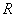 ≥ ≥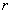 ) )
由由方程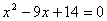 有 有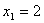 , ,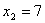
∴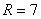 , ,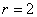
又∵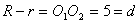
∴两圆的位置关系为内切。
变式:若方程变为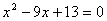 ,则两圆的位置关系如何? ,则两圆的位置关系如何?
分析:显然此方程的两根不易直接求出,用求根公式又麻烦了,考虑到要判断两圆的位置关系,只须将两圆半径的和、差与圆心距比较即可,我们可以用韦达定理,设两圆的半径分别为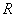 、 、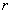 ( (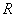 ≥ ≥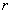 ),则 ),则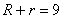 , ,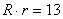 。 。
∴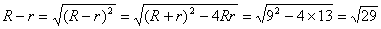
而O1O2=5<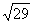 ,∴两圆的位置关系为内含。 ,∴两圆的位置关系为内含。
【例2】 如图,⊙O1与⊙O2外切于点P,AB过P点分别交⊙O1和⊙O2于A、B两点,BD切⊙O2于点B,交⊙O1于C、D两点,延长CP交⊙O2于Q。 (1)求证: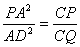 ; ; |

