|
25.圆与圆(二)
知识考点:
1、掌握两圆的内外公切线长的性质和求切线长的方法(转化为解直角三角形)。
2、掌握有关两圆的内、外公切线的基本图形,以及这类问题添加辅助线的方法,会结合圆的切线的性质解决有关两圆公切线的问题。
精典例题:
【例1】如图,⊙O1与⊙O2外切于P,AB是来两圆的外公切线,切点为A、B,我们称△PAB为切点三角形,切点三角形具有许多性质,现总结如下:
(1)△PAB是直角三角形,并且∠APB=900;
(2)△PAB的外接圆与连心线O1O2相切;
(3)以O1O2为直径的圆与Rt△PAB的斜边AB相切;
(4)斜边AB是两圆直径的比例中项;
(5)若⊙O1、⊙O2的半径为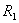 、 、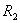 ,则PA∶PB∶AB= ,则PA∶PB∶AB=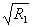 ∶ ∶ ∶ ∶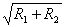 ; ;
(6)内公切线PC平分斜边AB;
(7)△CO1O2为直角三 角形。 角形。
这些结论虽然在证题时仍需证明,但有了这些基本结论作基础,可帮助你迅速找到解题思路,可以提高解题速度,下面用一个具体的例子来说明。
  
如图2,⊙A和⊙B外切于P,CD为两圆的外公切线,C、D分别为切点,PT为内公切线,PT与CD相交于点T,延长CP、DP分别与两圆相交于点E、F,又⊙A的半径为9,⊙B的半径为4。
(1)求PT的长;
(2)求证: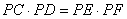 ; ;
(3)试在图中找出是线段PA和PB比例中项的线段,并加以证明。 分析:图中的基本图形是切点三角形,易证T为CD的中点,∠CPD=900,PT即为外公切线长的一半,CF、DE分别 |

