|
2010年中考数学二轮复习——代数几何综合题
Ⅰ、综合问题精讲:
代数几何综合题是初中数学中覆盖面最广、综合性最强的题型,近几年中考试题中的综合题大多以代数几何综合题的形式出现,其解题关键点是借助几何直观解题,运用方程、函数的思想解题,灵活运用数形结合,由形导数,以数促形,综合运用代数几何知识解题.
Ⅱ、典型例题剖析
【例1】(温州,12分)如图,已知四边形ABCD内接于⊙O,A是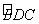 的中点,AE⊥AC于A,与⊙O及CB的延长线分别交于点F、E,且 的中点,AE⊥AC于A,与⊙O及CB的延长线分别交于点F、E,且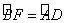 ,EM切⊙O于M。 ,EM切⊙O于M。
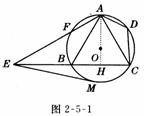 ⑴ △ADC∽△EBA;⑵ AC2=BC·CE; ⑴ △ADC∽△EBA;⑵ AC2=BC·CE;
⑶如果AB=2,EM=3,求cot∠CAD的值。
解:⑴∵四边形ABCD内接于⊙O,∴∠CDA=∠ABE,
∵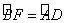 ,∴∠DCA=∠BAE, ,∴∠DCA=∠BAE,
∴△CAD∽△AEB
⑵ 过A作AH⊥BC于H(如图)
∵A是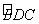 中点,∴HC=HB=BC, 中点,∴HC=HB=BC,
∵∠CAE=900,∴AC2=CH·CE=BC·CE
⑶∵A是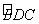 中点,AB=2,∴AC=AB=2, 中点,AB=2,∴AC=AB=2,
∵EM是⊙O的切线,∴EB·EC=EM2 ①
∵AC2=BC·CE,BC·CE=8 ②
①+②得:EC(EB+BC)=17,∴EC2=17
∵EC2=AC2+AE2,∴AE= ∵△CAD∽△ABE,∴∠ |

