|
函数在实际中的应用
函数在中考中具有重要的地位,近几年中考中出现很多与实际问题相结合的函数题目,注意实际问题和函数的转化。 例1.如图,一位运动员在距篮下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈,已知篮圈中心到地面的距离为3.05米。
(1)建立如图所示的直角坐标系,求抛物线的解析式。
(2)该运动员身高1.8米,在这次跳投中,球在头顶上方0.25米处出手,问:球出手时,他跳离地面的高度是多少?
分析:(1)已知,顶点(0,3.5)过一点(1.5,3.05)用顶点式。
(2)已知横坐标-2.5,求出纵坐标,就是抛出点的高度。
解:(1)由题意知抛物线顶点坐标为(0,3.5)且过(1.5,3.05)点,
∴设y=a(x-0)2+3.5
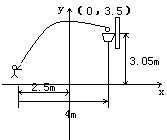 即y=ax2+3.5, 即y=ax2+3.5,
将(1.5, 3.05)代入,3.05=2.25a+3.5
2.25a=-0.45
a=-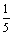
∴y=-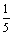 x2+3.5 x2+3.5
(2)当x=-2.5时,
y=-0.2×(-2.5)2+3.5=2.25
2.25-1.8-0.25=0.20(m)
答:球出手时,他距离地面高度是0.20m。
说明:求抛物线的解析式时,一定要正确找到抛物线上的点,并注意根据坐标系的位置,确定坐标的符号。
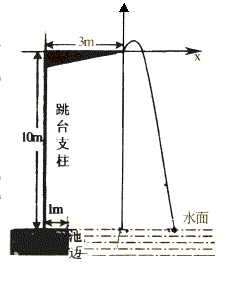 例2.某跳水运动员进行10米跳台跳 例2.某跳水运动员进行10米跳台跳 |

