|
图形折叠型问题解法浅析
折叠型问题是近年中考的热点问题,通常是把某个图形按照给定的条件折叠,通过折叠前后图形变换的相互关系来命题。折叠型问题立意新颖,变幻巧妙,对培养学生的识图能力及灵活运用数学知识解决问题的能力非常有效。下面我们一起来探究这种题型的解法。
折叠的规律是:折叠部分的图形,折叠前后,关于折痕成轴对称,两图形全等。
1.(2000,福建福州试卷)
如图,长方形ABCD沿AE折叠,使D落在边BC上的F点处,如果∠BAF=60°,则
 ∠DAE=___。 ∠DAE=___。
答案:A,15°
分析 根据折叠的规律:可证△ADE≌△AFE,从而
∠DAE=∠FAE=(90°-60°)÷2=150
A.15° B.30° C.45° D.60°
2.(济南市2000年中考试题)
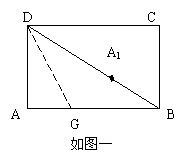 如图,折叠矩形纸片ABCD,先折出折痕(对角线)BD,再折叠,使AD落在对角线BD上,得折痕DG,若AB = 2,BC = 1,求AG. 如图,折叠矩形纸片ABCD,先折出折痕(对角线)BD,再折叠,使AD落在对角线BD上,得折痕DG,若AB = 2,BC = 1,求AG.
答案:AG =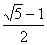
分析 折叠后的图形(如图一),
设A点落在BD上的位置为A1,
则 A 点关于直线 DG 的对称点为点 A1,
连结 A1G,(如图二)
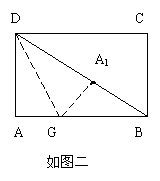 可知△ADG ≌ △A1DG,AG = A1G, 可知△ADG ≌ △A1DG,AG = A1G,
AD = A1D。∵矩形ABCD,AB = 2,
BC = 1,∴BD =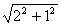 = =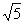 , ,
BA1 = 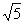 –1,∵∠ BA1G = ∠ A = 90°。 –1,∵∠ BA1G = ∠ A = 90°。
设AG = A1G= X,在Rt△BA1G中,
利用勾股定理列出方程:x2 +(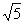 –1)2 = ( 2 – x )2, –1)2 = ( 2 – x )2,
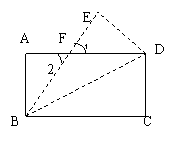 ∴ x = ∴ x = 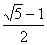 ,即:AG = ,即:AG =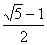 . .
|

