|
2011年中考数学复习知识讲解+例题解析+强化训练
一元二次方程
◆知识讲解
1.一元二次方程的一般形式ax2+bx+c=0(a,b,c是常数,a≠0)
2.一元二次方程的解法
(1)直接开平方法;(2)配方法;(3)公式法;(4)因式分解法.一元二次方程的求根公式是
x=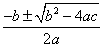 (b2-4ac≥0). (b2-4ac≥0).
3.二元三项式ax2+bx+c=a(x-x1)(x-x2).其中x1,x2是关于x的方程ax2+bx+c=0的两个实数根.
4.一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac.当△>0时,方程有两个不相等的实数根x1=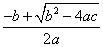 ,x2= ,x2=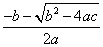 ;当△=0时,方程有两个相等实数根x1=x2=- ;当△=0时,方程有两个相等实数根x1=x2=-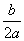 ;当△<0时,方程没有实数根. ;当△<0时,方程没有实数根.
5.若一元二次方程ax2+bx+c=0(a≠0)的两个实数根为x1,x2,则x1+x2=-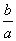 ,x1x2= ,x1x2=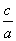 . .
6.以x1,x2为根的一元二次方程可写成x2-(x1+x2)x+x1x2=0.
7.使用一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac解题的前提是二次项系数a≠0.
8.若x1,x2是关于x的方程ax2+bx+c=0的两根,则ax12+bx1+c=0,ax22+bx2+c=0.反之,若ax12+bx1+c=0,ax22+bx2+c=0,且x1≠x2,则x1,x2是关于x的一元二次方程ax2+bx+c=0的两根.
9.一元二次方程的应用
列一元二次方程解应用问题的步骤和解法与前面讲过的列方程解应用题的方法步骤相同,但在解题中心须注意所求出的方程的解一定要使实际问题有意义,凡不满足实际问题的解(虽然是原方程的解)一定要舍去.
◆例题解析 |

